Točno
25. svibnja 2013. 20:47 (12 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Dokazimo tvrdnju matematickom indukcijom:
Za k=0 tvrdnja vrijedi - mozemo odabrati brojeve 1, 2, 4, 5.
Pretpostavimo da tvrdnja vrijedi za neki prirodan broj n.
Dokazimo da tada vrijedi i za n+1.
Podijelimo niz prvih 5*3^(n+1) brojeva u tri podniza uzastopnih brojeva svaki duljine 5*3^n. U prvom podnizu mozemo odabrati 4*2^n brojeva medju kojima nikoja tri ne tvore aritmeticki niz. To mozemo uciniti i u zadnjem podnizu - jednostavno uvecamo svaki broj iz odabranih u prvom podnizu za 10*3^n. Primijetimo jos da je razlika svakih dvaju brojeva iz istog podniza manja od 5*3^n, a svakih dvaju iz razlicitih podnizova veca od 5*3^n (promatramo samo prvi i zadnji podniz). Time smo odabrali 4*2^(n+1) brojeva od kojih nikoja tri ne cine aritmeticki niz.
Za k=0 tvrdnja vrijedi - mozemo odabrati brojeve 1, 2, 4, 5.
Pretpostavimo da tvrdnja vrijedi za neki prirodan broj n.
Dokazimo da tada vrijedi i za n+1.
Podijelimo niz prvih 5*3^(n+1) brojeva u tri podniza uzastopnih brojeva svaki duljine 5*3^n. U prvom podnizu mozemo odabrati 4*2^n brojeva medju kojima nikoja tri ne tvore aritmeticki niz. To mozemo uciniti i u zadnjem podnizu - jednostavno uvecamo svaki broj iz odabranih u prvom podnizu za 10*3^n. Primijetimo jos da je razlika svakih dvaju brojeva iz istog podniza manja od 5*3^n, a svakih dvaju iz razlicitih podnizova veca od 5*3^n (promatramo samo prvi i zadnji podniz). Time smo odabrali 4*2^(n+1) brojeva od kojih nikoja tri ne cine aritmeticki niz.
 Školjka
Školjka 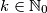 moguće odabrati
moguće odabrati 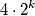 različitih prirodnih brojeva koji nisu veći od
različitih prirodnih brojeva koji nisu veći od 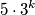 , tako da među njima ne postoje tri uzastopna člana aritmetičkog niza.
, tako da među njima ne postoje tri uzastopna člana aritmetičkog niza.