Prvo rješenje.
Dani uvjet je ekvivalentan uvjetu 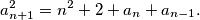 Pretpostavimo da su za neke
Pretpostavimo da su za neke  i
i  svi članovi niza racionalni. Neka su
svi članovi niza racionalni. Neka su  i
i  nizovi prirodnih brojeva takvi da su
nizovi prirodnih brojeva takvi da su 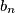 i
i 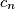 relativno prosti za svaki
relativno prosti za svaki  i takvi da je
i takvi da je 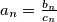 . Tada rekurziju možemo zapisati kao
. Tada rekurziju možemo zapisati kao 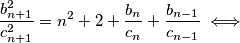
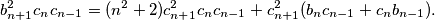 Iz ovog možemo zaključiti da
Iz ovog možemo zaključiti da 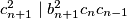 , a kako su
, a kako su 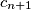 i
i 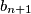 relativno prosti, vrijedi
relativno prosti, vrijedi 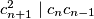 .
.
Iz ovog slijedi 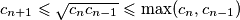 , a kako je
, a kako je 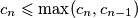 , vrijedi
, vrijedi  , pa je to padajući niz prirodnih brojeva, pa postoje prirodni brojevi
, pa je to padajući niz prirodnih brojeva, pa postoje prirodni brojevi  i
i  takvi da vrijedi
takvi da vrijedi 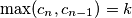 za svaki
za svaki 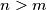 .
.
Promotrimo neki 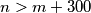 . Ako je
. Ako je 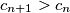 , onda je
, onda je 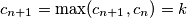 , ali je i
, ali je i 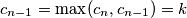 . Međutim, tada je
. Međutim, tada je 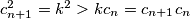 , što je kontradikcija. Dakle,
, što je kontradikcija. Dakle, 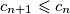 za svaki
za svaki 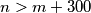 .
.
Iz toga slijedi da je 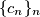 padajući niz prirodnih brojeva, pa postoje
padajući niz prirodnih brojeva, pa postoje  i
i  takvi da je
takvi da je 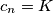 za svaki
za svaki 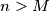 .
.
Tada za svaki osim konačno mnogo  vrijedi
vrijedi 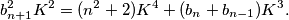 Iz ovog slijedi
Iz ovog slijedi 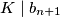 , ali
, ali  i
i 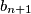 su relativno prosti, pa vrijedi
su relativno prosti, pa vrijedi 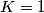 .
.
Sada za svaki 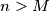 vrijedi
vrijedi 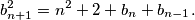 Desna strana je veća od
Desna strana je veća od 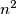 , pa mora vrijediti
, pa mora vrijediti 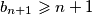 . To znači da postoji beskonačno prirodnih brojeva
. To znači da postoji beskonačno prirodnih brojeva  takvih da je
takvih da je 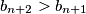 jer je niz
jer je niz 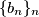 neograničen.
neograničen.
Promotrimo takav 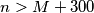 i oduzmimo izraze
i oduzmimo izraze 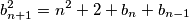
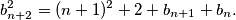 Dobivamo da vrijedi
Dobivamo da vrijedi 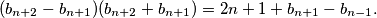 Lijeva strana je veća ili jednaka
Lijeva strana je veća ili jednaka 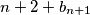 , a desna strana je manja ili jednaka
, a desna strana je manja ili jednaka 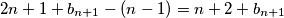 , zbog nejednakosti
, zbog nejednakosti 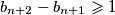 ,
,

i
 . Jednakost se postiže ako i samo ako vrijede jednakosti
. Jednakost se postiže ako i samo ako vrijede jednakosti 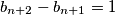 ,
, 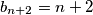 i
i 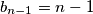 .
.
Iz ovog slijedi 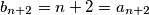 i
i 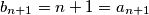 . Kako za svaki
. Kako za svaki 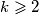 vrijedi
vrijedi 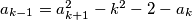 ,
, 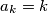 i
i 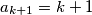 implicira
implicira 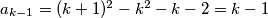 , pa induktivno vrijedi i
, pa induktivno vrijedi i 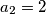 te
te 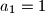 .
.
Iz ovog slijedi da je 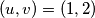 jedino moguće rješenje. Direktnom provjerom vidimo da niz
jedino moguće rješenje. Direktnom provjerom vidimo da niz 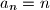 zadovoljava rekurziju pa je
zadovoljava rekurziju pa je 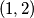 uistinu rješenje.
uistinu rješenje.
Drugo rješenje.
Uvedemo nizove 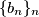 i
i 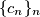 kao u prvom rješenju, te ponovno dobijemo
kao u prvom rješenju, te ponovno dobijemo 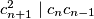 .
.
Neka je  prost broj koji dijeli
prost broj koji dijeli 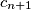 . Tada taj prost broj dijeli
. Tada taj prost broj dijeli 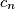 ili
ili 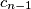 , pa zaključujemo da svaki prost broj koji dijeli
, pa zaključujemo da svaki prost broj koji dijeli 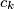 za neki
za neki  mora dijeliti
mora dijeliti 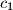 ili
ili 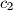 , pa niz ima konačno mnogo prostih faktora.
, pa niz ima konačno mnogo prostih faktora.
Promotrimo sada neki prost broj  koji dijeli neki član niza. Neka je
koji dijeli neki član niza. Neka je 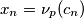 . Tada vrijedi
. Tada vrijedi 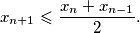 Ako je
Ako je 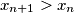 , onda je
, onda je 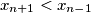 , pa vrijedi
, pa vrijedi  . To je padajući niz nenegativnih cijelih brojeva, pa postoje prirodan broj
. To je padajući niz nenegativnih cijelih brojeva, pa postoje prirodan broj 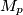 i nenegativan cijeli broj
i nenegativan cijeli broj 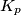 takav da je
takav da je 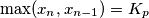 za svaki
za svaki 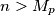 .
.
Promotrimo neki 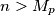 . Ako je
. Ako je 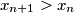 , onda je
, onda je 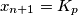 jer
jer 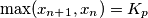 , ali je i
, ali je i 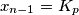 jer je
jer je 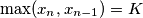 . Međutim,
. Međutim, 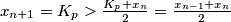 , što je kontradikcija.
, što je kontradikcija.
Dakle, 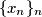 je također padajući niz nenegativnih cijelih brojeva, pa postoje
je također padajući niz nenegativnih cijelih brojeva, pa postoje 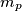 i
i 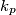 takvi da je
takvi da je 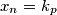 za svaki
za svaki 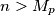 .
.
Kako ima konačno mnogo prostih faktora  niza
niza 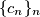 i svaki od prostih faktora vrijedi da se niz
i svaki od prostih faktora vrijedi da se niz 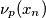 stabilizira, iz ovog slijedi da postoje
stabilizira, iz ovog slijedi da postoje  i
i  takvi da je
takvi da je 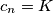 za svaki
za svaki 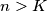 .
.
Tada za svaki osim konačno mnogo  vrijedi
vrijedi 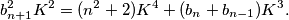 Iz ovog slijedi
Iz ovog slijedi 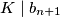 , ali
, ali  i
i 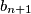 su relativno prosti, pa vrijedi
su relativno prosti, pa vrijedi 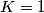 .
.
Sada za svaki 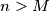 vrijedi
vrijedi 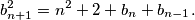 Desna strana je veća od
Desna strana je veća od 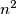 , pa mora vrijediti
, pa mora vrijediti 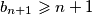 . Definirajmo niz
. Definirajmo niz 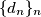 tako da je
tako da je 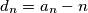 . Tada se rekurzija može zapisati kao
. Tada se rekurzija može zapisati kao 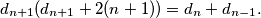 Iz ovog slijedi
Iz ovog slijedi 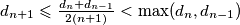 , pa je niz
, pa je niz 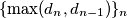 padajući, pa se stabilizira, ali se onda stabilizira i
padajući, pa se stabilizira, ali se onda stabilizira i 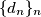 , odnosno jednak je
, odnosno jednak je  za beskonačno
za beskonačno  . Tada vrijedi
. Tada vrijedi 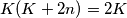 , pa je nužno
, pa je nužno 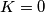 , jer je inače lijeva strana veća od desne za dovoljno velik
, jer je inače lijeva strana veća od desne za dovoljno velik  .
.
Iz ovog slijedi 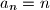 za svaki
za svaki  dovoljno velik, pa kao i u prethodnom rješenju zaključujemo
dovoljno velik, pa kao i u prethodnom rješenju zaključujemo 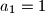 i
i 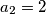 .
.
{\textbf{Prvo rješenje.}}
Dani uvjet je ekvivalentan uvjetu $$a_{n+1}^2=n^2+2+a_n+a_{n-1}.$$ Pretpostavimo da su za neke $u$ i $v$ svi članovi niza racionalni. Neka su $\{b_n\}_n$ i $\{c_n\}_n$ nizovi prirodnih brojeva takvi da su $b_n$ i $c_n$ relativno prosti za svaki $n$ i takvi da je $a_n=\frac{b_n}{c_n}$. Tada rekurziju možemo zapisati kao $$\frac{b_{n+1}^2}{c_{n+1}^2}=n^2+2+\frac{b_n}{c_n}+\frac{b_{n-1}}{c_{n-1}} \iff $$ $$b_{n+1}^2c_nc_{n-1}=(n^2+2)c_{n+1}^2c_nc_{n-1}+c_{n+1}^2(b_nc_{n-1}+c_nb_{n-1}).$$ Iz ovog možemo zaključiti da $c_{n+1}^2 \mid b_{n+1}^2c_nc_{n-1}$, a kako su $c_{n+1}$ i $b_{n+1}$ relativno prosti, vrijedi $c_{n+1}^2 \mid c_nc_{n-1}$. \\
Iz ovog slijedi $c_{n+1}\leqslant \sqrt{c_nc_{n-1}} \leqslant \max(c_n,c_{n-1})$, a kako je $c_n\leqslant \max(c_n,c_{n-1})$, vrijedi $\max(c_{n+1},c_n) \leqslant \max(c_n, c_{n-1})$, pa je to padajući niz prirodnih brojeva, pa postoje prirodni brojevi $m$ i $k$ takvi da vrijedi $\max(c_{n},c_{n-1})=k$ za svaki $n>m$. \\
Promotrimo neki $n>m+300$. Ako je $c_{n+1}>c_n$, onda je $c_{n+1}=\max(c_{n+1},c_n)=k$, ali je i $c_{n-1}=\max(c_n,c_{n-1})=k$. Međutim, tada je $c_{n+1}^2=k^2>kc_{n}=c_{n+1}c_n$, što je kontradikcija. Dakle, $c_{n+1}\leqslant c_n$ za svaki $n>m+300$. \\ Iz toga slijedi da je $\{c_n\}_n$ padajući niz prirodnih brojeva, pa postoje $M$ i $K$ takvi da je $c_n=K$ za svaki $n>M$. \\
Tada za svaki osim konačno mnogo $n$ vrijedi $$b_{n+1}^2K^2=(n^2+2)K^4+(b_n+b_{n-1})K^3.$$ Iz ovog slijedi $K \mid b_{n+1}$, ali $K$ i $b_{n+1}$ su relativno prosti, pa vrijedi $K=1$. \\ Sada za svaki $n>M$ vrijedi $$b_{n+1}^2=n^2+2+b_n+b_{n-1}.$$ Desna strana je veća od $n^2$, pa mora vrijediti $b_{n+1}\geqslant n+1$.
To znači da postoji beskonačno prirodnih brojeva $n$ takvih da je $b_{n+2}>b_{n+1}$ jer je niz $\{b_n\}_n$ neograničen. \\Promotrimo takav $n>M+300$ i oduzmimo izraze $$ b_{n+1}^2=n^2+2+b_n+b_{n-1}$$ $$ b_{n+2}^2=(n+1)^2+2+b_{n+1}+b_{n}.$$ Dobivamo da vrijedi $$(b_{n+2}-b_{n+1})(b_{n+2}+b_{n+1})=2n+1+b_{n+1}-b_{n-1}.$$ Lijeva strana je veća ili jednaka $n+2+b_{n+1}$, a desna strana je manja ili jednaka $2n+1+b_{n+1}-(n-1)=n+2+b_{n+1}$, zbog nejednakosti $b_{n+2}-b_{n+1}\geqslant 1$, \\ $b_{n+2}\geqslant n+2$ \\ i \\ $b_{n-1} \geqslant n-1$. Jednakost se postiže ako i samo ako vrijede jednakosti $b_{n+2}-b_{n+1}=1$, $b_{n+2}=n+2$ i $b_{n-1}=n-1$. \\ Iz ovog slijedi $b_{n+2}=n+2=a_{n+2}$ i $b_{n+1}=n+1=a_{n+1}$. Kako za svaki $k\geqslant 2$ vrijedi $a_{k-1}=a_{k+1}^2-k^2-2-a_k$, $a_{k}=k$ i $a_{k+1}=k+1$ implicira $a_{k-1}=(k+1)^2-k^2-k-2=k-1$, pa induktivno vrijedi i $a_2=2$ te $a_1=1$.\\ Iz ovog slijedi da je $(u,v)=(1,2)$ jedino moguće rješenje. Direktnom provjerom vidimo da niz $a_n=n$ zadovoljava rekurziju pa je $(1,2)$ uistinu rješenje. \\
{\textbf{Drugo rješenje.}}
Uvedemo nizove $\{b_n\}_n$ i $\{c_n\}_n$ kao u prvom rješenju, te ponovno dobijemo $c_{n+1}^2 \mid c_nc_{n-1}$. \\
Neka je $p$ prost broj koji dijeli $c_{n+1}$. Tada taj prost broj dijeli $c_n$ ili $c_{n-1}$, pa zaključujemo da svaki prost broj koji dijeli $c_k$ za neki $k$ mora dijeliti $c_1$ ili $c_2$, pa niz ima konačno mnogo prostih faktora. \\
Promotrimo sada neki prost broj $p$ koji dijeli neki član niza. Neka je $x_n=\nu_p(c_n)$.
Tada vrijedi $$x_{n+1}\leqslant \frac{x_n+x_{n-1}}{2}.$$ Ako je $x_{n+1} > x_n$, onda je $x_{n+1}<x_{n-1}$, pa vrijedi $\max(x_{n+1},x_n)\leqslant \max(x_n,x_{n-1})$. To je padajući niz nenegativnih cijelih brojeva, pa postoje prirodan broj $M_p$ i nenegativan cijeli broj $K_p$ takav da je $\max(x_n,x_{n-1})=K_p$ za svaki $n>M_p$. \\ Promotrimo neki $n>M_p$. Ako je $x_{n+1}>x_n$, onda je $x_{n+1}=K_p$ jer $\max(x_{n+1},x_n)=K_p$, ali je i $x_{n-1}=K_p$ jer je $\max(x_n,x_{n-1})=K$. Međutim, $x_{n+1}=K_p>\frac{K_p+x_n}{2}=\frac{x_{n-1}+x_n}{2}$, što je kontradikcija. \\ Dakle, $\{x_n\}_n$ je također padajući niz nenegativnih cijelih brojeva, pa postoje $m_p$ i $k_p$ takvi da je $x_n=k_p$ za svaki $n>M_p$. \\
Kako ima konačno mnogo prostih faktora $p$ niza $\{c_n\}_n$ i svaki od prostih faktora vrijedi da se niz $\nu_p(x_n)$ stabilizira, iz ovog slijedi da postoje $M$ i $K$ takvi da je $c_n=K$ za svaki $n>K$. \\
Tada za svaki osim konačno mnogo $n$ vrijedi $$b_{n+1}^2K^2=(n^2+2)K^4+(b_n+b_{n-1})K^3.$$ Iz ovog slijedi $K \mid b_{n+1}$, ali $K$ i $b_{n+1}$ su relativno prosti, pa vrijedi $K=1$. \\
Sada za svaki $n>M$ vrijedi $$b_{n+1}^2=n^2+2+b_n+b_{n-1}.$$ Desna strana je veća od $n^2$, pa mora vrijediti $b_{n+1}\geqslant n+1$. Definirajmo niz $\{d_n\}_n$ tako da je $d_n=a_n-n$.
Tada se rekurzija može zapisati kao $$d_{n+1}(d_{n+1}+2(n+1))=d_{n}+d_{n-1}.$$ Iz ovog slijedi $d_{n+1}\leqslant \frac{d_n+d_{n-1}}{2(n+1)}<\max(d_n,d_{n-1})$, pa je niz $\{\max(d_n,d_{n-1})\}_n$ padajući,
pa se stabilizira, ali se onda stabilizira i $\{d_n\}_n$, odnosno jednak je $K$ za beskonačno $n$. Tada vrijedi $K(K+2n)=2K$, pa je nužno $K=0$, jer je inače lijeva strana veća od desne za dovoljno velik $n$. \\
Iz ovog slijedi $a_n=n$ za svaki $n$ dovoljno velik, pa kao i u prethodnom rješenju zaključujemo $a_1=1$ i $a_2=2$.
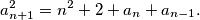 Pretpostavimo da su za neke
Pretpostavimo da su za neke 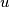 i
i  svi članovi niza racionalni. Neka su
svi članovi niza racionalni. Neka su 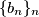 i
i 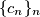 nizovi prirodnih brojeva takvi da su
nizovi prirodnih brojeva takvi da su 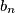 i
i 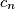 relativno prosti za svaki
relativno prosti za svaki  i takvi da je
i takvi da je 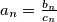 . Tada rekurziju možemo zapisati kao
. Tada rekurziju možemo zapisati kao 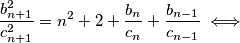
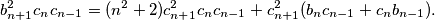 Iz ovog možemo zaključiti da
Iz ovog možemo zaključiti da 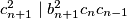 , a kako su
, a kako su 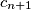 i
i 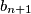 relativno prosti, vrijedi
relativno prosti, vrijedi 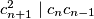 .
. 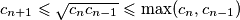 , a kako je
, a kako je 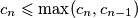 , vrijedi
, vrijedi  , pa je to padajući niz prirodnih brojeva, pa postoje prirodni brojevi
, pa je to padajući niz prirodnih brojeva, pa postoje prirodni brojevi  i
i  takvi da vrijedi
takvi da vrijedi 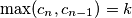 za svaki
za svaki 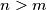 .
. 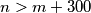 . Ako je
. Ako je 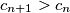 , onda je
, onda je 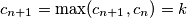 , ali je i
, ali je i 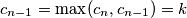 . Međutim, tada je
. Međutim, tada je 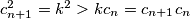 , što je kontradikcija. Dakle,
, što je kontradikcija. Dakle, 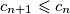 za svaki
za svaki 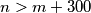 .
. 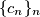 padajući niz prirodnih brojeva, pa postoje
padajući niz prirodnih brojeva, pa postoje  i
i  takvi da je
takvi da je 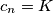 za svaki
za svaki 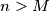 .
.  vrijedi
vrijedi 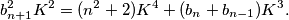 Iz ovog slijedi
Iz ovog slijedi 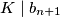 , ali
, ali  i
i 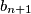 su relativno prosti, pa vrijedi
su relativno prosti, pa vrijedi 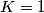 .
. 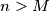 vrijedi
vrijedi 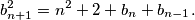 Desna strana je veća od
Desna strana je veća od 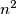 , pa mora vrijediti
, pa mora vrijediti 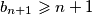 . To znači da postoji beskonačno prirodnih brojeva
. To znači da postoji beskonačno prirodnih brojeva  takvih da je
takvih da je 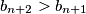 jer je niz
jer je niz 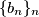 neograničen.
neograničen. 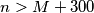 i oduzmimo izraze
i oduzmimo izraze 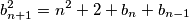
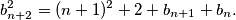 Dobivamo da vrijedi
Dobivamo da vrijedi 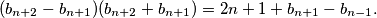 Lijeva strana je veća ili jednaka
Lijeva strana je veća ili jednaka 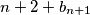 , a desna strana je manja ili jednaka
, a desna strana je manja ili jednaka 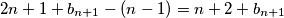 , zbog nejednakosti
, zbog nejednakosti 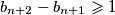 ,
, 
 . Jednakost se postiže ako i samo ako vrijede jednakosti
. Jednakost se postiže ako i samo ako vrijede jednakosti 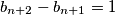 ,
, 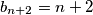 i
i 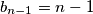 .
. 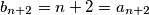 i
i 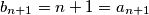 . Kako za svaki
. Kako za svaki 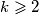 vrijedi
vrijedi 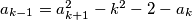 ,
, 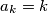 i
i 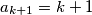 implicira
implicira 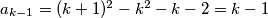 , pa induktivno vrijedi i
, pa induktivno vrijedi i 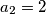 te
te 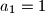 .
.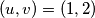 jedino moguće rješenje. Direktnom provjerom vidimo da niz
jedino moguće rješenje. Direktnom provjerom vidimo da niz 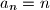 zadovoljava rekurziju pa je
zadovoljava rekurziju pa je 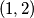 uistinu rješenje.
uistinu rješenje. 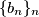 i
i 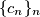 kao u prvom rješenju, te ponovno dobijemo
kao u prvom rješenju, te ponovno dobijemo 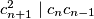 .
.  prost broj koji dijeli
prost broj koji dijeli 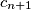 . Tada taj prost broj dijeli
. Tada taj prost broj dijeli 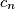 ili
ili 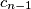 , pa zaključujemo da svaki prost broj koji dijeli
, pa zaključujemo da svaki prost broj koji dijeli 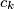 za neki
za neki  mora dijeliti
mora dijeliti 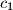 ili
ili 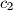 , pa niz ima konačno mnogo prostih faktora.
, pa niz ima konačno mnogo prostih faktora.  koji dijeli neki član niza. Neka je
koji dijeli neki član niza. Neka je 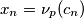 . Tada vrijedi
. Tada vrijedi 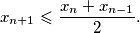 Ako je
Ako je 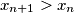 , onda je
, onda je 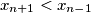 , pa vrijedi
, pa vrijedi  . To je padajući niz nenegativnih cijelih brojeva, pa postoje prirodan broj
. To je padajući niz nenegativnih cijelih brojeva, pa postoje prirodan broj 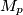 i nenegativan cijeli broj
i nenegativan cijeli broj 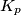 takav da je
takav da je 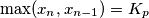 za svaki
za svaki 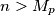 .
. 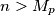 . Ako je
. Ako je 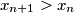 , onda je
, onda je 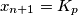 jer
jer 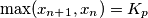 , ali je i
, ali je i 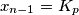 jer je
jer je 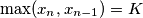 . Međutim,
. Međutim, 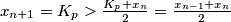 , što je kontradikcija.
, što je kontradikcija. 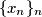 je također padajući niz nenegativnih cijelih brojeva, pa postoje
je također padajući niz nenegativnih cijelih brojeva, pa postoje 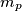 i
i 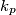 takvi da je
takvi da je 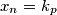 za svaki
za svaki 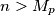 .
.  niza
niza 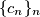 i svaki od prostih faktora vrijedi da se niz
i svaki od prostih faktora vrijedi da se niz 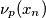 stabilizira, iz ovog slijedi da postoje
stabilizira, iz ovog slijedi da postoje  i
i  takvi da je
takvi da je 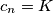 za svaki
za svaki 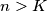 .
.  vrijedi
vrijedi 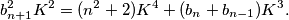 Iz ovog slijedi
Iz ovog slijedi 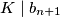 , ali
, ali  i
i 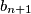 su relativno prosti, pa vrijedi
su relativno prosti, pa vrijedi 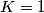 .
. 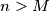 vrijedi
vrijedi 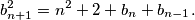 Desna strana je veća od
Desna strana je veća od 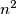 , pa mora vrijediti
, pa mora vrijediti 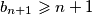 . Definirajmo niz
. Definirajmo niz 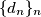 tako da je
tako da je 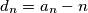 . Tada se rekurzija može zapisati kao
. Tada se rekurzija može zapisati kao 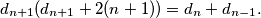 Iz ovog slijedi
Iz ovog slijedi 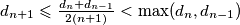 , pa je niz
, pa je niz 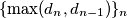 padajući, pa se stabilizira, ali se onda stabilizira i
padajući, pa se stabilizira, ali se onda stabilizira i 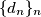 , odnosno jednak je
, odnosno jednak je  za beskonačno
za beskonačno  . Tada vrijedi
. Tada vrijedi 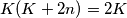 , pa je nužno
, pa je nužno 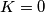 , jer je inače lijeva strana veća od desne za dovoljno velik
, jer je inače lijeva strana veća od desne za dovoljno velik  .
. 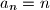 za svaki
za svaki  dovoljno velik, pa kao i u prethodnom rješenju zaključujemo
dovoljno velik, pa kao i u prethodnom rješenju zaključujemo 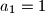 i
i 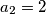 .
.  Školjka
Školjka 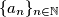 rekurzivno tako da vrijedi
rekurzivno tako da vrijedi 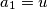 ,
, 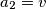 , te za svaki prirodan broj
, te za svaki prirodan broj 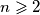 vrijedi
vrijedi 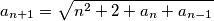 Odredi sve parove
Odredi sve parove 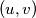 za koje je
za koje je  racionalan za svaki prirodan broj
racionalan za svaki prirodan broj