Neocijenjeno
2. studenoga 2019. 23:23 (6 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Imamo 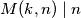 za sve
za sve 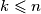 , pa sumu s lijeve strane možemo prikazati kao sumu po djeliteljima
, pa sumu s lijeve strane možemo prikazati kao sumu po djeliteljima  . Potrebno je izračunati, za neki
. Potrebno je izračunati, za neki 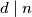 , koliko postoji
, koliko postoji 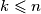 takvih da
takvih da 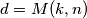 .
.
Međutim, tada je očito 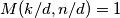 i vrijedi
i vrijedi  , ali i za svaki
, ali i za svaki 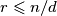 takav da
takav da 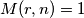 je
je 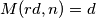 , pa je dovoljno naći koliko ima takvih
, pa je dovoljno naći koliko ima takvih  , a to je upravo
, a to je upravo 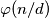 . Prema tome, imamo:
. Prema tome, imamo: 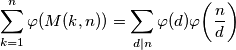 Dovoljno je sada pokazati da
Dovoljno je sada pokazati da 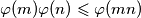 .
.
Međutim, kako 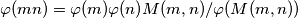 i
i 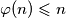 , ovo je očito.
, ovo je očito.
Jednakost vrijedi kad u svakoj od prethodnih nejednakosti vrijedi jednakost, to jest, kada su 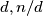 relativno prosti za sve vrijednosti
relativno prosti za sve vrijednosti 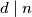 , to jest kad je
, to jest kad je  kvadratno slobodan.
kvadratno slobodan.
 Školjka
Školjka 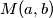 najveći zajednički djelitelj prirodnih brojeva
najveći zajednički djelitelj prirodnih brojeva 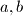 . Neka je
. Neka je 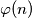 broj prirodnih brojeva
broj prirodnih brojeva 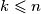 takvih da
takvih da 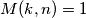 , a neka je
, a neka je 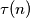 broj djeljitelja
broj djeljitelja