Prvo rješenje.
Tvrdimo da je odgovor 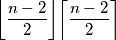 .
.
Dokažimo da se taj broj može postići. Označimo bakterije s 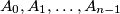 tako da je
tako da je  kraljica.
kraljica.
Postavimo da su 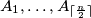 djeca od
djeca od  , te da su ostale bakterije djeca od
, te da su ostale bakterije djeca od 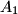 .
.
Tada je svaka kći od  različita od
različita od  teta svakoj kćeri od
teta svakoj kćeri od  , pa ih ima
, pa ih ima 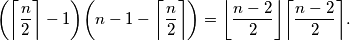
Označimo kraljicu s  . Za bakteriju
. Za bakteriju  različitu od kraljice, neka je
različitu od kraljice, neka je 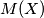 majka od
majka od  . Tada definiramo dubinu od
. Tada definiramo dubinu od  kao najmanji
kao najmanji  takav da je
takav da je 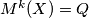 , te stavimo da je dubina od
, te stavimo da je dubina od  jednaka
jednaka  . Broj parova (tetka, nećakinja) je manji ili jednak broju parova bakterija
. Broj parova (tetka, nećakinja) je manji ili jednak broju parova bakterija 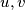 takvih da je dubina od
takvih da je dubina od  različite parnosti od dubine od
različite parnosti od dubine od  i takvih da
i takvih da  i
i  nisu spojeni, jer tetka i nećakinja imaju dubine različite parnosti i nisu spojene.
nisu spojeni, jer tetka i nećakinja imaju dubine različite parnosti i nisu spojene.
Neka je  broj bakterija parne dubine. Tada je broj opisanih parova jednak
broj bakterija parne dubine. Tada je broj opisanih parova jednak 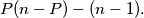 Lijevi pribrojnik je broj parova različite dubine, a od tog broja moramo oduzeti one povezane, a ima
Lijevi pribrojnik je broj parova različite dubine, a od tog broja moramo oduzeti one povezane, a ima  bridova. Taj broj je prema AG nejednakosti manji ili jednak
bridova. Taj broj je prema AG nejednakosti manji ili jednak 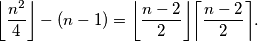 Iz toga slijedi da je i broj parova (tetka, nećakinja) ograničen tim brojem, kao što je i trebalo pokazati.
Iz toga slijedi da je i broj parova (tetka, nećakinja) ograničen tim brojem, kao što je i trebalo pokazati.
Drugo rješenje.
Konstrukcija je ista kao i u prvom rješenju. Dubinu definiramo kao i u prvom rješenju. Neka je 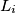 broj vrhova s dubinom
broj vrhova s dubinom  .
.
Vrijedi da je broj parova (teta, nećakinja) manji ili jednak broju parova 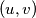 takvih da je dubina od
takvih da je dubina od  za
za  manja od dubine od
manja od dubine od  i takvih da
i takvih da  nije majka od
nije majka od  . Naime, ako su neki
. Naime, ako su neki 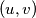 teta i nećakinja, tada je dubina od
teta i nećakinja, tada je dubina od  za
za  manja od dubine od
manja od dubine od  i
i  nije majka od
nije majka od  . Vrijedi da je broj opisanih parova jednak
. Vrijedi da je broj opisanih parova jednak 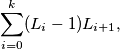 gdje je
gdje je  maksimalna dubina, zato što neki vrh čija dubina je
maksimalna dubina, zato što neki vrh čija dubina je 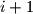 se spari s točno
se spari s točno 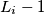 vrhova dubine
vrhova dubine  , sa svima čija dubina je
, sa svima čija dubina je  osim sa svojom majkom.
osim sa svojom majkom.
Primijetimo da vrijedi 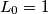 pa prvi pribrojnik možemo zanemariti. Također,
pa prvi pribrojnik možemo zanemariti. Također,  pa možemo i zadnji pribrojnik zanemariti. Nadalje, vrijedi
pa možemo i zadnji pribrojnik zanemariti. Nadalje, vrijedi 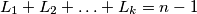 . Uvedimo oznaku
. Uvedimo oznaku 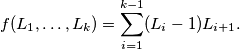
Dokažimo matematičkom indukcijom po  sljedeću tvrdnju:
sljedeću tvrdnju:
Za svaki prirodan broj 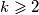 , za svaki prirodan broj
, za svaki prirodan broj 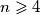 i za svakih
i za svakih  prirodnih brojeva
prirodnih brojeva 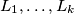 za koje vrijedi
za koje vrijedi 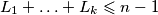 , vrijedi
, vrijedi 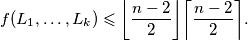 Baza: za
Baza: za 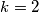 , vrijedi
, vrijedi 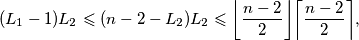 gdje zadnja nejednakost slijedi iz AG nejednakosti.
gdje zadnja nejednakost slijedi iz AG nejednakosti.
Pretpostavimo da tvrdnja vrijedi za  , gdje je
, gdje je 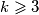 . Promotrimo brojeve
. Promotrimo brojeve 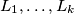 čiji zbroj je manji ili jednak
čiji zbroj je manji ili jednak  .
.
Pretpostavimo da je 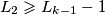 . Tada vrijedi
. Tada vrijedi 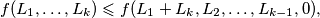 jer je
jer je 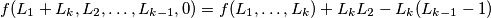 . Nova
. Nova  -torka zadovoljava sve uvjete (zbroj je ostao isti, svi brojevi su prirodni), pa možemo primijeniti pretpostavku indukcije pa vrijedi nejednakost.
-torka zadovoljava sve uvjete (zbroj je ostao isti, svi brojevi su prirodni), pa možemo primijeniti pretpostavku indukcije pa vrijedi nejednakost.
Drugi slučaj je ako je 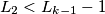 . Tada vrijedi
. Tada vrijedi 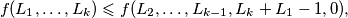 gdje nejednakost vrijedi zbog
gdje nejednakost vrijedi zbog 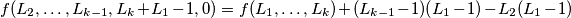 . Nova
. Nova  -torka zadovoljava sve uvjete (zbroj se smanjio za
-torka zadovoljava sve uvjete (zbroj se smanjio za  , svi brojevi su prirodni), pa po pretpostavci indukcije i u ovom slučaju vrijedi nejednakost. Time smo pokazali korak indukcije.
, svi brojevi su prirodni), pa po pretpostavci indukcije i u ovom slučaju vrijedi nejednakost. Time smo pokazali korak indukcije.
Dakle, broj parova (tetka, nećakinja) je manji ili jednak od 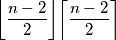 , čime smo dokazali da je to maksimum.
, čime smo dokazali da je to maksimum.
{\textbf{Prvo rješenje.}}
\\
Tvrdimo da je odgovor $\bigg \lfloor \dfrac{n-2}{2} \bigg \rfloor \bigg \lceil \dfrac{n-2}{2} \bigg \rceil$. \\
Dokažimo da se taj broj može postići. Označimo bakterije s $A_0,A_1,\ldots,A_{n-1}$ tako da je $A_0$ kraljica. \\Postavimo da su $A_1,\ldots,A_{\lceil \frac{n}{2} \rceil}$ djeca od $A_0$, te da su ostale bakterije djeca od $A_{1}$. \\Tada je svaka kći od $A_0$ različita od $A_1$ teta svakoj kćeri od $A_1$, pa ih ima $$\bigg (\bigg \lceil \dfrac{n}{2} \bigg \rceil-1\bigg )\bigg(n-1- \bigg \lceil \dfrac{n}{2} \bigg \rceil\bigg)=\bigg \lfloor \dfrac{n-2}{2} \bigg \rfloor \bigg \lceil \dfrac{n-2}{2} \bigg \rceil.$$ \\
Označimo kraljicu s $Q$. Za bakteriju $X$ različitu od kraljice, neka je $M(X)$ majka od $X$. Tada definiramo dubinu od $X$ kao najmanji $k$ takav da je $M^k(X)=Q$, te stavimo da je dubina od $Q$ jednaka $0$. Broj parova (tetka, nećakinja) je manji ili jednak broju parova bakterija ${u,v}$ takvih da je dubina od $u$ različite parnosti od dubine od $v$ i takvih da $u$ i $v$ nisu spojeni, jer tetka i nećakinja imaju dubine različite parnosti i nisu spojene. \\ Neka je $P$ broj bakterija parne dubine.
Tada je broj opisanih parova jednak $$P(n-P)-(n-1).$$ Lijevi pribrojnik je broj parova različite dubine, a od tog broja moramo oduzeti one povezane, a ima $n-1$ bridova. Taj broj je prema AG nejednakosti manji ili jednak $$\bigg \lfloor \frac{n^2}{4} \bigg \rfloor -(n-1)=\bigg \lfloor \dfrac{n-2}{2} \bigg \rfloor \bigg \lceil \dfrac{n-2}{2} \bigg \rceil.$$ Iz toga slijedi da je i broj parova (tetka, nećakinja) ograničen tim brojem, kao što je i trebalo pokazati. \\
{\textbf{Drugo rješenje.}}
Konstrukcija je ista kao i u prvom rješenju. Dubinu definiramo kao i u prvom rješenju. Neka je $L_i$ broj vrhova s dubinom $i$. \\
Vrijedi da je broj parova (teta, nećakinja) manji ili jednak broju parova $(u,v)$ takvih da je dubina od $u$ za $1$ manja od dubine od $v$ i takvih da $u$ nije majka od $v$. Naime, ako su neki $(u,v)$ teta i nećakinja, tada je dubina od $u$ za $1$ manja od dubine od $v$ i $u$ nije majka od $v$.
Vrijedi da je broj opisanih parova jednak $$\sum_{i=0}^{k} (L_i-1)L_{i+1},$$ gdje je $k$ maksimalna dubina, zato što neki vrh čija dubina je $i+1$ se spari s točno $L_i-1$ vrhova dubine $i$, sa svima čija dubina je $i$ osim sa svojom majkom. \\ Primijetimo da vrijedi $L_0=1$ pa prvi pribrojnik možemo zanemariti. Također, $L_{k+1}=0$ pa možemo i zadnji pribrojnik zanemariti. Nadalje, vrijedi $L_1+L_2+\ldots+L_k=n-1$. Uvedimo oznaku $$f(L_1,\ldots,L_k)=\sum_{i=1}^{k-1} (L_i-1)L_{i+1}.$$ \\
Dokažimo matematičkom indukcijom po $k$ sljedeću tvrdnju: \\
\emph{Za svaki prirodan broj $k\geqslant2$, za svaki prirodan broj $n\geqslant 4$ i za svakih $k$ prirodnih brojeva $L_1,\ldots,L_k$ za koje vrijedi $L_1+\ldots+L_k\leqslant n-1$, vrijedi $$f(L_1,\ldots,L_k)\leqslant \bigg \lfloor \dfrac{n-2}{2} \bigg \rfloor \bigg \lceil \dfrac{n-2}{2} \bigg \rceil. $$} Baza: za $k=2$, vrijedi $$(L_1-1)L_2 \leqslant (n-2-L_2)L_2 \leqslant \bigg \lfloor \dfrac{n-2}{2} \bigg \rfloor \bigg \lceil \dfrac{n-2}{2} \bigg \rceil,$$ gdje zadnja nejednakost slijedi iz AG nejednakosti. \\
Pretpostavimo da tvrdnja vrijedi za $k-1$, gdje je $k\geqslant 3$. Promotrimo brojeve $L_1,\ldots,L_k$ čiji zbroj je manji ili jednak $n-1$. \\
Pretpostavimo da je $L_2\geqslant L_{k-1}-1$. Tada vrijedi $$f(L_1,\ldots,L_k)\leqslant f(L_1+L_k, L_2,\ldots, L_{k-1},0),$$ jer je $f(L_1+L_k, L_2,\ldots, L_{k-1},0)=f(L_1,\ldots,L_k)+L_kL_2-L_k(L_{k-1}-1)$. Nova $k-1$-torka zadovoljava sve uvjete (zbroj je ostao isti, svi brojevi su prirodni), pa možemo primijeniti pretpostavku indukcije pa vrijedi nejednakost. \\
Drugi slučaj je ako je $L_2<L_{k-1}-1$. Tada vrijedi $$f(L_1,\ldots,L_k)\leqslant f(L_2,\ldots, L_{k-1},L_k+L_1-1,0),$$ gdje nejednakost vrijedi zbog $f(L_2,\ldots, L_{k-1},L_k+L_1-1,0)=f(L_1,\ldots,L_k)+(L_{k-1}-1)(L_1-1)-L_2(L_1-1)$. Nova $k-1$-torka zadovoljava sve uvjete (zbroj se smanjio za $1$, svi brojevi su prirodni), pa po pretpostavci indukcije i u ovom slučaju vrijedi nejednakost. Time smo pokazali korak indukcije. \\
Dakle, broj parova (tetka, nećakinja) je manji ili jednak od $\bigg \lfloor \dfrac{n-2}{2} \bigg \rfloor \bigg \lceil \dfrac{n-2}{2} \bigg \rceil$, čime smo dokazali da je to maksimum.
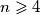 prirodan broj. Promotrimo skup od
prirodan broj. Promotrimo skup od  bakterija, takav da svaka bakterija osim jedne, koju ćemo zvati Kraljica, ima točno jednu majku (također bakteriju iz skupa). Kraljica nema niti jednu majku te je predak svim drugim bakterijama. Nijedna bakterija nije majka sama sebi. Kažemo da je bakterija
bakterija, takav da svaka bakterija osim jedne, koju ćemo zvati Kraljica, ima točno jednu majku (također bakteriju iz skupa). Kraljica nema niti jednu majku te je predak svim drugim bakterijama. Nijedna bakterija nije majka sama sebi. Kažemo da je bakterija  tetka bakterije
tetka bakterije  ako
ako  nije majka od
nije majka od  i majka od
i majka od  je majka majke od
je majka majke od  . Odredi maksimalan broj parova bakterija
. Odredi maksimalan broj parova bakterija 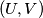 takvih da je
takvih da je  tetka od
tetka od  .
. predak bakterije
predak bakterije  ako postoji niz bakterija
ako postoji niz bakterija 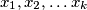 takav da
takav da 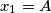 ,
, 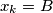 te je
te je 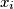 majka
majka 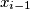 za svaki
za svaki 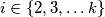 )
) 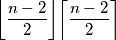 .
. 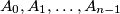 tako da je
tako da je  kraljica.
kraljica. 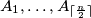 djeca od
djeca od  , te da su ostale bakterije djeca od
, te da su ostale bakterije djeca od 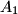 .
.  različita od
različita od  teta svakoj kćeri od
teta svakoj kćeri od  , pa ih ima
, pa ih ima 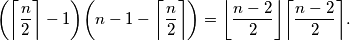
 . Za bakteriju
. Za bakteriju  različitu od kraljice, neka je
različitu od kraljice, neka je 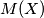 majka od
majka od  . Tada definiramo dubinu od
. Tada definiramo dubinu od  kao najmanji
kao najmanji  takav da je
takav da je 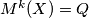 , te stavimo da je dubina od
, te stavimo da je dubina od  jednaka
jednaka  . Broj parova (tetka, nećakinja) je manji ili jednak broju parova bakterija
. Broj parova (tetka, nećakinja) je manji ili jednak broju parova bakterija 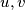 takvih da je dubina od
takvih da je dubina od  različite parnosti od dubine od
različite parnosti od dubine od  i takvih da
i takvih da  i
i  nisu spojeni, jer tetka i nećakinja imaju dubine različite parnosti i nisu spojene.
nisu spojeni, jer tetka i nećakinja imaju dubine različite parnosti i nisu spojene.  broj bakterija parne dubine. Tada je broj opisanih parova jednak
broj bakterija parne dubine. Tada je broj opisanih parova jednak 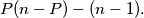 Lijevi pribrojnik je broj parova različite dubine, a od tog broja moramo oduzeti one povezane, a ima
Lijevi pribrojnik je broj parova različite dubine, a od tog broja moramo oduzeti one povezane, a ima  bridova. Taj broj je prema AG nejednakosti manji ili jednak
bridova. Taj broj je prema AG nejednakosti manji ili jednak 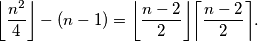 Iz toga slijedi da je i broj parova (tetka, nećakinja) ograničen tim brojem, kao što je i trebalo pokazati.
Iz toga slijedi da je i broj parova (tetka, nećakinja) ograničen tim brojem, kao što je i trebalo pokazati. 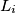 broj vrhova s dubinom
broj vrhova s dubinom  .
. 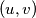 takvih da je dubina od
takvih da je dubina od  za
za  manja od dubine od
manja od dubine od  i takvih da
i takvih da  nije majka od
nije majka od  . Naime, ako su neki
. Naime, ako su neki 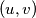 teta i nećakinja, tada je dubina od
teta i nećakinja, tada je dubina od  za
za  manja od dubine od
manja od dubine od  i
i  nije majka od
nije majka od  . Vrijedi da je broj opisanih parova jednak
. Vrijedi da je broj opisanih parova jednak 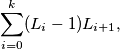 gdje je
gdje je  maksimalna dubina, zato što neki vrh čija dubina je
maksimalna dubina, zato što neki vrh čija dubina je 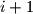 se spari s točno
se spari s točno 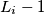 vrhova dubine
vrhova dubine  , sa svima čija dubina je
, sa svima čija dubina je  osim sa svojom majkom.
osim sa svojom majkom. 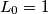 pa prvi pribrojnik možemo zanemariti. Također,
pa prvi pribrojnik možemo zanemariti. Također,  pa možemo i zadnji pribrojnik zanemariti. Nadalje, vrijedi
pa možemo i zadnji pribrojnik zanemariti. Nadalje, vrijedi 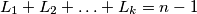 . Uvedimo oznaku
. Uvedimo oznaku 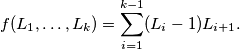
 sljedeću tvrdnju:
sljedeću tvrdnju: 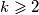 , za svaki prirodan broj
, za svaki prirodan broj 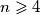 i za svakih
i za svakih  prirodnih brojeva
prirodnih brojeva 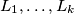 za koje vrijedi
za koje vrijedi 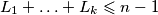 , vrijedi
, vrijedi 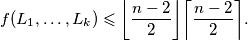 Baza: za
Baza: za 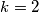 , vrijedi
, vrijedi 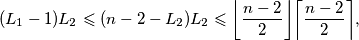 gdje zadnja nejednakost slijedi iz AG nejednakosti.
gdje zadnja nejednakost slijedi iz AG nejednakosti.  , gdje je
, gdje je 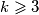 . Promotrimo brojeve
. Promotrimo brojeve 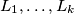 čiji zbroj je manji ili jednak
čiji zbroj je manji ili jednak  .
. 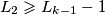 . Tada vrijedi
. Tada vrijedi 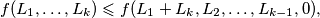 jer je
jer je 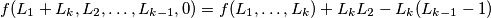 . Nova
. Nova  -torka zadovoljava sve uvjete (zbroj je ostao isti, svi brojevi su prirodni), pa možemo primijeniti pretpostavku indukcije pa vrijedi nejednakost.
-torka zadovoljava sve uvjete (zbroj je ostao isti, svi brojevi su prirodni), pa možemo primijeniti pretpostavku indukcije pa vrijedi nejednakost. 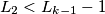 . Tada vrijedi
. Tada vrijedi 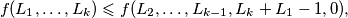 gdje nejednakost vrijedi zbog
gdje nejednakost vrijedi zbog 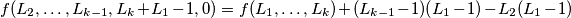 . Nova
. Nova  -torka zadovoljava sve uvjete (zbroj se smanjio za
-torka zadovoljava sve uvjete (zbroj se smanjio za  , svi brojevi su prirodni), pa po pretpostavci indukcije i u ovom slučaju vrijedi nejednakost. Time smo pokazali korak indukcije.
, svi brojevi su prirodni), pa po pretpostavci indukcije i u ovom slučaju vrijedi nejednakost. Time smo pokazali korak indukcije. 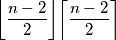 , čime smo dokazali da je to maksimum.
, čime smo dokazali da je to maksimum.  Školjka
Školjka