Prvo rješenje. (Ivan Novak)
Mora vrijediti 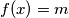 za sve
za sve 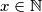 .
.
Dokažimo da za svaki prirodan broj 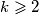 vrijedi:
vrijedi: 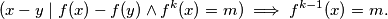 Definirajmo
Definirajmo 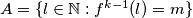 ,
, 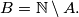 Ako je
Ako je  prazan, nema se što dokazivati. Pretpostavimo da je
prazan, nema se što dokazivati. Pretpostavimo da je  neprazan i izaberimo proizvoljne brojeve
neprazan i izaberimo proizvoljne brojeve 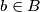 ,
, 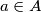 . Primijetimo da za svaki
. Primijetimo da za svaki 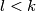 vrijedi
vrijedi 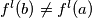 . Zbog toga vrijedi redom
. Zbog toga vrijedi redom 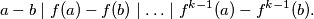 Kako je
Kako je 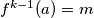 , vrijedi
, vrijedi 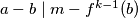 .
.
Kako je 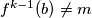 , vrijedi
, vrijedi 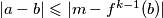 .
.
Ako je skup  beskonačan, možemo fiksirati
beskonačan, možemo fiksirati  i izabrati dovoljno velik
i izabrati dovoljno velik 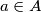 takav da zadnja nejednakost ne vrijedi.
takav da zadnja nejednakost ne vrijedi.
Ako je  konačan, tada je
konačan, tada je  beskonačan. Primijetimo da za svaki
beskonačan. Primijetimo da za svaki 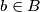 vrijedi
vrijedi 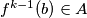 . Iz toga slijedi da je
. Iz toga slijedi da je 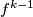 ograničena odozgo najvećim elementom skupa
ograničena odozgo najvećim elementom skupa  . Kako je
. Kako je  beskonačan, možemo fiksirati
beskonačan, možemo fiksirati  i uvrstiti dovoljno velik
i uvrstiti dovoljno velik 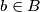 takav da zadnja nejednakost ne vrijedi.
takav da zadnja nejednakost ne vrijedi.
Dakle,  je nužno prazan, pa je tvrdnja dokazana. Primjenom dokazane tvrdnje
je nužno prazan, pa je tvrdnja dokazana. Primjenom dokazane tvrdnje 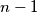 puta dolazimo do zaključka da je
puta dolazimo do zaključka da je 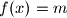 za svaki
za svaki 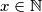 .
.
Drugo rješenje. (Borna Šimić)
Mora vrijediti 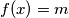 za sve
za sve 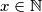 .
.
Pretpostavimo suprotno, da postoji 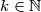 takav da
takav da 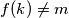 . Tada za svaki
. Tada za svaki  različit od
različit od 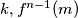 imamo:
imamo: 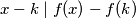
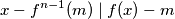 Budući da
Budući da 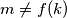 , barem jedan of
, barem jedan of 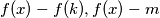 nije nula. Prema tome, za svaki
nije nula. Prema tome, za svaki 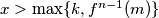 postoje
postoje 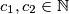 za koje vrijedi
za koje vrijedi 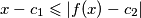 Ako
Ako 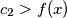 , vrijedi
, vrijedi 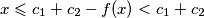 . Prema tome, uzmemo li
. Prema tome, uzmemo li 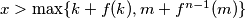 , mora vrijediti
, mora vrijediti 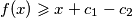 . Uzmemo li
. Uzmemo li 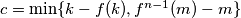 dobivamo
dobivamo 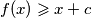 za sve
za sve 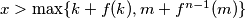 .
.
Međutim, tada 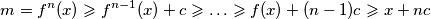 za svaki
za svaki  dovoljno velik, što je očito nemoguće, pa u ovom slučaju nema rješenja.
dovoljno velik, što je očito nemoguće, pa u ovom slučaju nema rješenja.
{\textbf{Prvo rješenje. (Ivan Novak)}}
Mora vrijediti $f(x) = m$ za sve $x\in \mathbb{N}$.
Dokažimo da za svaki prirodan broj $k\geqslant 2$ vrijedi: $$(x - y \mid f(x) - f(y) \land f^k(x)=m) \implies f^{k-1}(x)=m.$$
Definirajmo $A=\{l \in \mathbb{N} : f^{k-1}(l)=m\}$, $B=\mathbb{N} \setminus A.$ Ako je $B$ prazan, nema se što dokazivati. Pretpostavimo da je $B$ neprazan i izaberimo proizvoljne brojeve $b\in B$, $a\in A$. Primijetimo da za svaki $l<k$ vrijedi $f^{l}(b)\neq f^{l}(a)$. Zbog toga vrijedi redom $$a-b \mid f(a)-f(b) \mid \ldots \mid f^{k-1}(a)-f^{k-1}(b).$$
Kako je $f^{k-1}(a)=m$, vrijedi $a-b \mid m-f^{k-1}(b)$.
\\ Kako je $f^{k-1}(b) \neq m$, vrijedi $|a-b|\leqslant |m-f^{k-1}(b)|$. \\
Ako je skup $A$ beskonačan, možemo fiksirati $b$ i izabrati dovoljno velik $a\in A$ takav da zadnja nejednakost ne vrijedi.\\
Ako je $A$ konačan, tada je $B$ beskonačan. Primijetimo da za svaki $b\in B$ vrijedi $f^{k-1}(b)\in A$. Iz toga slijedi da je $f^{k-1}$ ograničena odozgo najvećim elementom skupa $A$. Kako je $B$ beskonačan, možemo fiksirati $a$ i uvrstiti dovoljno velik $b\in B$ takav da zadnja nejednakost ne vrijedi. \\
Dakle, $B$ je nužno prazan, pa je tvrdnja dokazana. Primjenom dokazane tvrdnje $n-1$ puta dolazimo do zaključka da je $f(x)=m$ za svaki $x\in \mathbb{N}$.
{\textbf{Drugo rješenje. (Borna Šimić)}}
Mora vrijediti $f(x) = m$ za sve $x\in \mathbb{N}$.
Pretpostavimo suprotno, da postoji $k \in \mathbb{N}$ takav da $f(k) \neq m$. Tada za svaki $x$ različit od $k, f^{n-1}(m)$ imamo:
$$x - k \mid f(x) - f(k)$$
$$x - f^{n-1}(m) \mid f(x) - m$$
Budući da $m \neq f(k)$, barem jedan of $f(x) - f(k), f(x) - m$ nije nula. Prema tome, za svaki $x > \max \{k, f^{n-1}(m)\}$ postoje $c_1, c_2 \in \mathbb{N}$ za koje vrijedi $$x - c_1 \leqslant |f(x) - c_2|$$
Ako $c_2 > f(x)$, vrijedi $x \leqslant c_1+c_2-f(x) < c_1 + c_2$.
Prema tome, uzmemo li $x > \max\{k+f(k), m+f^{n-1}(m)\}$, mora vrijediti $f(x) \geqslant x + c_1 - c_2$.
Uzmemo li $c = \min \{k-f(k), f^{n-1}(m)-m\}$ dobivamo $$f(x) \geqslant x + c$$ za sve $x > \max\{k+f(k), m+f^{n-1}(m)\}$.
Međutim, tada $$m = f^n(x) \geqslant f^{n-1}(x) + c \geqslant \ldots \geqslant f(x) + (n-1)c \geqslant x + nc$$ za svaki $x$ dovoljno velik, što je očito nemoguće, pa u ovom slučaju nema rješenja.
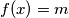 za sve
za sve 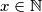 .
.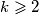 vrijedi:
vrijedi: 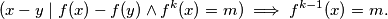 Definirajmo
Definirajmo 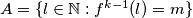 ,
, 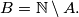 Ako je
Ako je  prazan, nema se što dokazivati. Pretpostavimo da je
prazan, nema se što dokazivati. Pretpostavimo da je  neprazan i izaberimo proizvoljne brojeve
neprazan i izaberimo proizvoljne brojeve 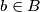 ,
, 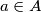 . Primijetimo da za svaki
. Primijetimo da za svaki 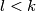 vrijedi
vrijedi 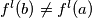 . Zbog toga vrijedi redom
. Zbog toga vrijedi redom 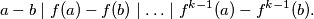 Kako je
Kako je 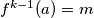 , vrijedi
, vrijedi 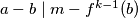 .
. 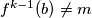 , vrijedi
, vrijedi 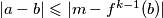 .
.  beskonačan, možemo fiksirati
beskonačan, možemo fiksirati  i izabrati dovoljno velik
i izabrati dovoljno velik 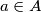 takav da zadnja nejednakost ne vrijedi.
takav da zadnja nejednakost ne vrijedi. konačan, tada je
konačan, tada je  beskonačan. Primijetimo da za svaki
beskonačan. Primijetimo da za svaki 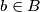 vrijedi
vrijedi 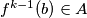 . Iz toga slijedi da je
. Iz toga slijedi da je 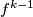 ograničena odozgo najvećim elementom skupa
ograničena odozgo najvećim elementom skupa  . Kako je
. Kako je  beskonačan, možemo fiksirati
beskonačan, možemo fiksirati  i uvrstiti dovoljno velik
i uvrstiti dovoljno velik 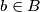 takav da zadnja nejednakost ne vrijedi.
takav da zadnja nejednakost ne vrijedi.  je nužno prazan, pa je tvrdnja dokazana. Primjenom dokazane tvrdnje
je nužno prazan, pa je tvrdnja dokazana. Primjenom dokazane tvrdnje 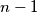 puta dolazimo do zaključka da je
puta dolazimo do zaključka da je 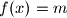 za svaki
za svaki 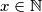 .
.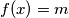 za sve
za sve 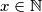 .
.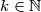 takav da
takav da 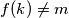 . Tada za svaki
. Tada za svaki  različit od
različit od 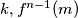 imamo:
imamo: 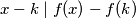
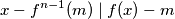 Budući da
Budući da 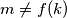 , barem jedan of
, barem jedan of 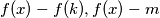 nije nula. Prema tome, za svaki
nije nula. Prema tome, za svaki 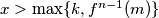 postoje
postoje 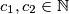 za koje vrijedi
za koje vrijedi 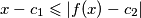 Ako
Ako 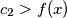 , vrijedi
, vrijedi 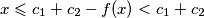 . Prema tome, uzmemo li
. Prema tome, uzmemo li 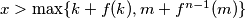 , mora vrijediti
, mora vrijediti 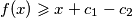 . Uzmemo li
. Uzmemo li 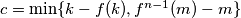 dobivamo
dobivamo 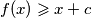 za sve
za sve 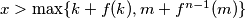 .
.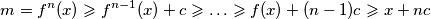 za svaki
za svaki  dovoljno velik, što je očito nemoguće, pa u ovom slučaju nema rješenja.
dovoljno velik, što je očito nemoguće, pa u ovom slučaju nema rješenja.  Školjka
Školjka  i
i  . Ako je
. Ako je 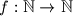 funkcija takva da za svaki
funkcija takva da za svaki 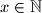 vrijedi
vrijedi 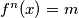 i da za sve različite
i da za sve različite 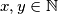 vrijedi
vrijedi 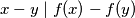 mora li vrijediti
mora li vrijediti