Sakrij rješenje
Neka je  konačan skup točaka u ravnini. Neka je
konačan skup točaka u ravnini. Neka je 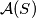 skup pravaca pridruženih skupu
skup pravaca pridruženih skupu  takav da je za svaki
takav da je za svaki 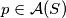 suma kvadrata udaljenosti točaka iz
suma kvadrata udaljenosti točaka iz  od
od  minimalna.
minimalna.
a) Ako je  osnosimetričan s obzirom na pravac
osnosimetričan s obzirom na pravac  i nema točaka na
i nema točaka na  , mora li neki
, mora li neki 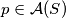 biti osnosimetričan s obzirom na
biti osnosimetričan s obzirom na  ?
?
b) Ako je  centralnosimetričan s obzirom na točku
centralnosimetričan s obzirom na točku  i ne sadrži
i ne sadrži  , mora li svaki
, mora li svaki 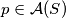 biti centralnosimetričan s obzirom na
biti centralnosimetričan s obzirom na  ?
?
(Borna Šimić)
Kliknite ovdje kako biste prikazali rješenje.
a) Barem jedan od pravaca mora biti osnosimetričan odnosno biti ili okomit na os simetrije ili sama os simetrije.
Postavimo Kartezijev koordinatni sustav tako da neki od pravaca koji su rješenja prolaze kroz ishodište i tako da je  -os os simetrije skupa
-os os simetrije skupa  .
.
Neka su 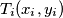 i
i 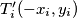 ,
, 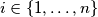 elementi skupa
elementi skupa  .
.
Zbroj udaljenosti elemenata skupa  od
od  -osi je
-osi je 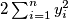 . Označimo tu sumu s
. Označimo tu sumu s 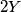 .
.
Zbroj udaljenosti elemenata skupa  od
od  -osi je
-osi je 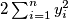 . Označino tu sumu s
. Označino tu sumu s 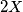 .
.
Ostale pravce kroz ishodište možemo prikazati u implicitnom obliku kao 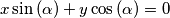 . Kvadrat udaljenosti točke
. Kvadrat udaljenosti točke 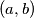 od takvog pravca je dan formulom
od takvog pravca je dan formulom 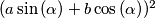 .
.
Sada primjenom te formule na točke iz  dobivamo da je traženi zbroj kvadrata udaljenosti jednak
dobivamo da je traženi zbroj kvadrata udaljenosti jednak 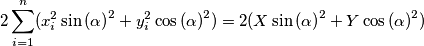
Dokažimo 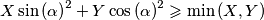 . Bez smanjenja općenitosti možemo pretpostaviti
. Bez smanjenja općenitosti možemo pretpostaviti 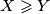 . Tada vrijedi
. Tada vrijedi 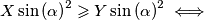
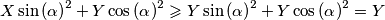 kao što smo i htjeli pokazati. Dakle,
kao što smo i htjeli pokazati. Dakle, 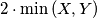 je minimalna suma kvadrata udaljenosti. Time je dokaz završen.
je minimalna suma kvadrata udaljenosti. Time je dokaz završen.
b) Svaki pravac mora biti centralnosimetričan, to jest, prolaziti kroz centar simetrije.
Označimo sumu kvadrata udaljenosti točaka iz skupa od pravca  sa
sa 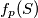 . Podijelimo točke u parove na taj način da
. Podijelimo točke u parove na taj način da 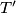 označava točku centralnosimetričnu sa
označava točku centralnosimetričnu sa  i primijetimo da
i primijetimo da 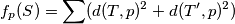 Fiksirajmo smjer pravca i promatramo neku klasu paralelnih pravaca. Za svaki par
Fiksirajmo smjer pravca i promatramo neku klasu paralelnih pravaca. Za svaki par 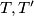 je
je 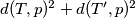 očito minimalno kad pravac prolazi između
očito minimalno kad pravac prolazi između 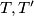 (inače ga možemo približiti obje točke istodobno). Za pravce između
(inače ga možemo približiti obje točke istodobno). Za pravce između  i
i 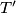 vrijedi
vrijedi 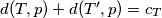 , i
, i 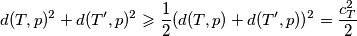 a minimum zbroja kvadrata udaljenosti se postiže kad su udaljenosti jednake, to jest kad pravac
a minimum zbroja kvadrata udaljenosti se postiže kad su udaljenosti jednake, to jest kad pravac  prolazi kroz polovište dužine
prolazi kroz polovište dužine 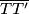 , što je ujedno i centar simetrije skupa
, što je ujedno i centar simetrije skupa  . Budući da se za svaki par
. Budući da se za svaki par  i
i 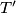 za fiksan smjer minimum postiže za isti pravac, minimum
za fiksan smjer minimum postiže za isti pravac, minimum 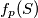 za klasu pravaca
za klasu pravaca  tog (i svakog drugog, analogno) smjera se postiže kad pravac prolazi kroz centar simetrije pa
tog (i svakog drugog, analogno) smjera se postiže kad pravac prolazi kroz centar simetrije pa 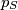 mora prolaziti kroz centar simetrije.
mora prolaziti kroz centar simetrije.
 Školjka
Školjka