Neocijenjeno
2. studenoga 2019. 23:53 (6 godine, 4 mjeseci)
Sakrij rješenje
Dan je trokut $ABC$. Neka su $M, N$ polovišta stranica $\overline{AB}, \overline{AC}$. Neka su $X, Y$ točke na simetralama stranica $\overline{AB}, \overline{AC}$ sa vanjske strane trokuta takve da $2|MX| = |AB|$ i $2|NY| = |AC|$. Neka je $Z$ nožište visine iz vrha $A$ u trokutu $ABC$. Dokaži da kružnica opisana trokutu $XYZ$ raspolavlja stranicu $\overline{BC}$.
\begin{flushright}\emph{(Borna Šimić)}\end{flushright}
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka su $\omega_B, \omega_C$ kružnice sa promjerima $\overline{AB}, \overline{AC}$. Tada vrijedi $X, Z \in \omega_B$ i $Y, Z \in \omega_C$. $X$ je polovište luka $\widehat{AB}$ kružnice $\omega_B$ pa je $XZ$ simetrala kuta $AZB$ te vrijedi $| \angle XZA | = 45^{\circ}$. Analogno, $| \angle YZA | = 45^{\circ}$ pa imamo:
$$| \angle XZY | = | \angle XZA | + | \angle YZA | = 90^{\circ}$$
Neka je $K$ presjek kružnice opisane trokutu $XYZ$ i pravca $BC$ različit od $Z$. Neka je $L$ presjek kružnice opisane trokutu $XYZ$ i pravca $AZ$ različit od $Z$. Zbog $| \angle XZA | = | \angle YZA | = 45^{\circ}$, $K$ je polovište luka $\widehat{XY}$. Zbog $| \angle KAL | = 90^{\circ}$, $\overline{KL}$ je promjer kružnice opisane trokutu $XYZ$ i okomit je na $XY$, pa je on simetrala $\overline{XY}$ te je $K$ presjek $BC$ i simetrale dužine $\overline{XY}$.
\\
Dokažimo sada da $K'$, polovište dužine $\overline{BC}$, leži na simetrali $\overline{XY}$. Promotrimo trokutove $XMK'$ i $YNK'$. Vrijedi:
$|MX| = \frac{|AB|}{2} = |NK'|$ i analogno $|NY| = |MK'|$. Također, imamo $| \angle XMK'| = 90^{\circ} + | \angle BAC| = | \angle YNK' |$ pa $\triangle XMK' \cong \triangle YNK'$ i vrijedi $|K'X| = |K'Y|$ pa se $K'$ nalazi na simetrali $\overline{XY}$ i vrijedi $K \equiv K'$ a time i $K'$ leži na kružnici opisanoj trokutu $XYZ$, što je i trebalo pokazati.
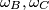 kružnice sa promjerima
kružnice sa promjerima 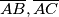 . Tada vrijedi
. Tada vrijedi 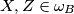 i
i 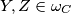 .
.  je polovište luka
je polovište luka 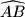 kružnice
kružnice  pa je
pa je 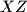 simetrala kuta
simetrala kuta 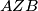 te vrijedi
te vrijedi 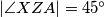 . Analogno,
. Analogno, 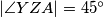 pa imamo:
pa imamo: 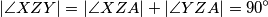 Neka je
Neka je  presjek kružnice opisane trokutu
presjek kružnice opisane trokutu 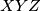 i pravca
i pravca  različit od
različit od  . Neka je
. Neka je  presjek kružnice opisane trokutu
presjek kružnice opisane trokutu 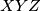 i pravca
i pravca 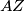 različit od
različit od  . Zbog
. Zbog 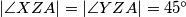 ,
,  je polovište luka
je polovište luka 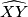 . Zbog
. Zbog 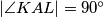 ,
, 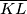 je promjer kružnice opisane trokutu
je promjer kružnice opisane trokutu 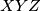 i okomit je na
i okomit je na  , pa je on simetrala
, pa je on simetrala 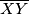 te je
te je  presjek
presjek  i simetrale dužine
i simetrale dužine 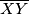 .
. 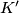 , polovište dužine
, polovište dužine  , leži na simetrali
, leži na simetrali 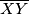 . Promotrimo trokutove
. Promotrimo trokutove 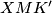 i
i 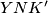 . Vrijedi:
. Vrijedi: 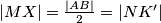 i analogno
i analogno 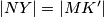 . Također, imamo
. Također, imamo 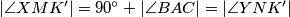 pa
pa 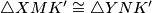 i vrijedi
i vrijedi 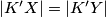 pa se
pa se 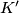 nalazi na simetrali
nalazi na simetrali 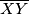 i vrijedi
i vrijedi 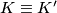 a time i
a time i 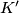 leži na kružnici opisanoj trokutu
leži na kružnici opisanoj trokutu 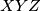 , što je i trebalo pokazati.
, što je i trebalo pokazati.  Školjka
Školjka  . Neka su
. Neka su 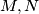 polovišta stranica
polovišta stranica 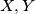 točke na simetralama stranica
točke na simetralama stranica 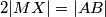 i
i 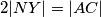 . Neka je
. Neka je  u trokutu
u trokutu