Sakrij rješenje
Kliknite ovdje kako biste prikazali rješenje.
Dokažimo da je  nužno oblika
nužno oblika 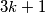 .
.
Promotrimo proizvoljan čvor  . Čvorove povezane s
. Čvorove povezane s  zvat ćemo susjedi od
zvat ćemo susjedi od  , a čvorove koji nisu povezani s
, a čvorove koji nisu povezani s  zvat ćemo nesusjedi od
zvat ćemo nesusjedi od  . Vezice patika ćemo zvati graf.
. Vezice patika ćemo zvati graf.
Promotrimo skup svih susjeda od  .
.  ima barem jednog susjeda jer svaka
ima barem jednog susjeda jer svaka  čvora imaju barem jednog zajedničkog susjeda. Svaki čvor koji je susjed od
čvora imaju barem jednog zajedničkog susjeda. Svaki čvor koji je susjed od  mora biti povezan s još točno
mora biti povezan s još točno  susjeda od
susjeda od  zbog prvog uvjeta zadatka.
zbog prvog uvjeta zadatka.
Pretpostavimo da je neki od tih susjeda  te da je povezan sa susjedima
te da je povezan sa susjedima  i
i  . Tada
. Tada  i
i  imaju
imaju  zajednička susjeda (
zajednička susjeda ( i
i  ) pa su i oni nužno povezani. Zaključujemo da su susjedi od
) pa su i oni nužno povezani. Zaključujemo da su susjedi od  podijeljeni u disjunktne tročlane skupove, pa je broj susjeda od
podijeljeni u disjunktne tročlane skupove, pa je broj susjeda od  djeljiv s
djeljiv s  .
.
Ako  nema nesusjeda, nema se što dokazivati. U suprotnom, svaki nesusjed od
nema nesusjeda, nema se što dokazivati. U suprotnom, svaki nesusjed od  je spojen s točno jednim susjedom od
je spojen s točno jednim susjedom od  zbog drugog uvjeta zadatka. Zbog toga možemo skup nesusjeda particionirati po tome s kojim su susjedom povezani.
zbog drugog uvjeta zadatka. Zbog toga možemo skup nesusjeda particionirati po tome s kojim su susjedom povezani.
Pretpostavimo da je neki susjed  spojen s nesusjedima
spojen s nesusjedima 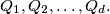
Tada  i
i 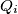 za svaki
za svaki 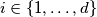 imaju još točno
imaju još točno  zajednička susjeda koji su ujedno i nesusjedi od
zajednička susjeda koji su ujedno i nesusjedi od  . Neka je neki
. Neka je neki 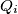 spojen s
spojen s 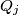 i
i 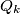 . Tada
. Tada 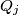 i
i 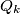 imaju
imaju  zajednička susjeda pa su nužno povezani. Vidimo da su
zajednička susjeda pa su nužno povezani. Vidimo da su 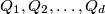 podijeljeni u disjunktne trojke, pa je
podijeljeni u disjunktne trojke, pa je  nužno djeljiv s
nužno djeljiv s  . Iz toga slijedi da je i broj nesusjeda nužno djeljiv s
. Iz toga slijedi da je i broj nesusjeda nužno djeljiv s  .
.
Dokažimo sada da za svaki  oblika
oblika 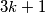 postoji graf s traženim svojstvima. Označimo vrhove s
postoji graf s traženim svojstvima. Označimo vrhove s 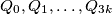 . Povežimo
. Povežimo 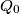 sa svim ostalim čvorovima te povežimo za svaki
sa svim ostalim čvorovima te povežimo za svaki 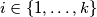 čvorove
čvorove 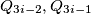 i
i 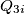 svaki sa svakim. Svaki taj tročlani skup zovimo grupica.
svaki sa svakim. Svaki taj tročlani skup zovimo grupica. 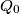 ima
ima  zajednička susjeda sa svakim od preostalih. Dva člana iste grupice imaju točno
zajednička susjeda sa svakim od preostalih. Dva člana iste grupice imaju točno  zajednička susjeda (
zajednička susjeda (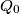 i preostali član grupice). Dva člana različitih grupica imaju točno jednog zajedničkog susjeda,
i preostali član grupice). Dva člana različitih grupica imaju točno jednog zajedničkog susjeda, 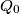 . Dakle, konstrukcija je valjana.
. Dakle, konstrukcija je valjana.
 Školjka
Školjka 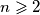 za koje je moguće da svaka
za koje je moguće da svaka 