Školjka Točno
31. kolovoza 2015. 02:16 (9 godine, 2 mjeseci)
, 
i 
novčića.Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
moze: ( 7, 9 , 11 ) --> ( 0 , 2 , 25 ) --> ( 2 , 1 , 24 ) --> ( 1 , 0 , 26 ), pa je na prvoj hrpi ostao jedan novicic :p
varijanta 2. "Moze li na kraju ostati samo jedna hrpa novcica?"
nemoze: gleda se broj novcica na nekoj hrpi modulo 3. na pocetku imamo module 0,1,2, a dana transformacija od svake hrpe ( gledano mod 3 ) oduzme jedan broj, dakle 0,1,2 salje u 2,0,1, itd. ==> nemoze se iz pocetnih 7,9,11 ~ 1,0,2 doci u zeljenih 0,0,0 ~ 0,0,27
edit (krivo/na brzinu procitan zadatak):
nemoze, jasno je da iz stanja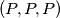
dolazimo u 
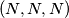te obratno dok radimo ovaj potez (sa 
i 
smo oznacili parnost broja novcica na pojedinoj hrpi). dakle, uvijek ce biti na sve tri hrpe neparan broj novcica ili na sve tri hrpe paran broj novcica, pa je nemoguce da na kraju ostane na jednoj hrpi jedan novcic a na ostale dvije po nula.
varijanta 2. "Moze li na kraju ostati samo jedna hrpa novcica?"
nemoze: gleda se broj novcica na nekoj hrpi modulo 3. na pocetku imamo module 0,1,2, a dana transformacija od svake hrpe ( gledano mod 3 ) oduzme jedan broj, dakle 0,1,2 salje u 2,0,1, itd. ==> nemoze se iz pocetnih 7,9,11 ~ 1,0,2 doci u zeljenih 0,0,0 ~ 0,0,27
edit (krivo/na brzinu procitan zadatak):
nemoze, jasno je da iz stanja
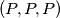dolazimo u 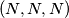te obratno dok radimo ovaj potez (sa i smo oznacili parnost broja novcica na pojedinoj hrpi). dakle, uvijek ce biti na sve tri hrpe neparan broj novcica ili na sve tri hrpe paran broj novcica, pa je nemoguce da na kraju ostane na jednoj hrpi jedan novcic a na ostale dvije po nula.