Točno
19. travnja 2012. 14:28 (12 godine, 7 mjeseci)
Neka su
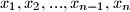
pozitivni realni brojevi takvi da je
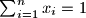
. Dokaži nejednakost
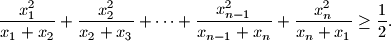
%V0
Neka su $x_1, x_2, . . . , x_{n-1}, x_n$ pozitivni realni brojevi takvi da je $\sum_{i=1}^{n}x_i = 1$. Dokaži nejednakost
$$\frac{x_1^2}{x_1+x_2} + \frac{x_2^2}{x_2+x_3} + \cdots + \frac{x_{n-1}^2}{x_{n-1}+x_n} + \frac{x_n^2}{x_n+x_1} \geq \frac{1}{2}.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Iz CSB nejednakosti slijedi da je
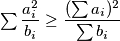
, a primjenom toga na ovu nejednakost, uz oznaku
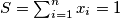
dolazimo do izraza
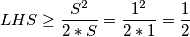
, čime je dokazana početna nejednakost.
%V0
Iz CSB nejednakosti slijedi da je $\sum{\dfrac{a_i^2}{b_i}} \geq \dfrac{(\sum a_i)^2}{\sum b_i}$, a primjenom toga na ovu nejednakost, uz oznaku $S = \sum_{i = 1}^n{x_i} = 1$ dolazimo do izraza $LHS \geq \dfrac{S^2}{2*S} = \dfrac{1^2}{2*1} = \dfrac{1}{2}$, čime je dokazana početna nejednakost. $\blacksquare$
| 19. travnja 2012. 15:54 | mljulj | Točno |
| 19. travnja 2012. 17:34 | grga | Točno |
Školjka