Jedine funkcije koje zadovoljavaju traženu jednakost su 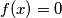 i
i 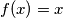 za sve realne
za sve realne  . Pretpostavimo da postoji
. Pretpostavimo da postoji  takav da
takav da 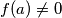 . tada uvrštavanjem
. tada uvrštavanjem 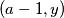 dobivamo da je f surjekcija.
dobivamo da je f surjekcija.
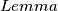 :
: 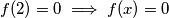 .
.
Pretpostavimo suprotno, uzmimo 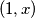 i imamo:
i imamo: 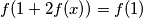 . Ali,
. Ali,  je surjektivna, pa lijeva strana može poprimiti oblik
je surjektivna, pa lijeva strana može poprimiti oblik 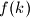 za bilo koji realni
za bilo koji realni  . Iz toga slijedi da je
. Iz toga slijedi da je  konstanta, neka je
konstanta, neka je 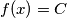 . Lagano se provjeri da može biti samo
. Lagano se provjeri da može biti samo 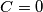 , suprotno pretpostavci.
, suprotno pretpostavci.
Uvrštavanjem 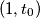 , gdje je
, gdje je 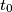 nultočka od
nultočka od  dobije se:
dobije se: 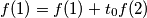 , pa je
, pa je 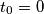
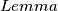 :
:  je injektivna
je injektivna
Pretpostavi 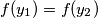 . Uvrštavanjem
. Uvrštavanjem 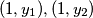 dobije se:
dobije se: 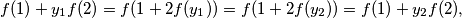 odakle
odakle 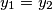
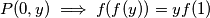 pa kad u to stavimo
pa kad u to stavimo 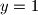 dobije se
dobije se 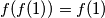 , odnosno
, odnosno 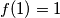 zbog injektivnosti. To povlači
zbog injektivnosti. To povlači 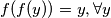
Fiksirajmo 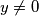 . Zbog toga što je
. Zbog toga što je  bijekcija i
bijekcija i 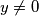 , postoji jedinstven
, postoji jedinstven  takav da
takav da 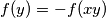 . Uvrštavanjem
. Uvrštavanjem 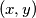 dobiva se:
dobiva se:
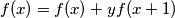 , te slijedi
, te slijedi 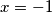 i
i 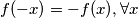 .
.
Konačno, za 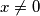 ,
, 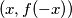 :
:
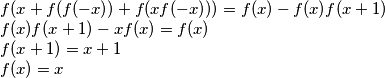 za sve
za sve 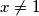 , a vrijedi i za
, a vrijedi i za  pa je
pa je 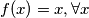
Jedine funkcije koje zadovoljavaju traženu jednakost su $f(x)=0$ i $f(x)=x$ za sve realne $x$.
Pretpostavimo da postoji $a$ takav da $f(a) \neq 0$. tada uvrštavanjem $(a-1, y)$ dobivamo da je f surjekcija.\\
$Lemma$: $f(2)=0 \implies f(x)=0$.\\
Pretpostavimo suprotno, uzmimo $(1, x)$ i imamo:
$f(1+2f(x))=f(1)$. Ali, $f$ je surjektivna, pa lijeva strana može poprimiti oblik $f(k)$ za bilo koji realni $k$. Iz toga slijedi da je $f$ konstanta, neka je $f(x)=C$. Lagano se provjeri da može biti samo $C=0$, suprotno pretpostavci.\\
Uvrštavanjem $(1, t_0)$, gdje je $t_0$ nultočka od $f$ dobije se:
$f(1)=f(1)+t_0f(2)$, pa je $t_0=0$
$Lemma$: $f$ je injektivna\\
Pretpostavi $f(y_1)=f(y_2)$. Uvrštavanjem $(1, y_1), (1, y_2)$ dobije se:
$f(1)+y_1f(2)=f(1+2f(y_1))=f(1+2f(y_2))=f(1)+y_2f(2), $ odakle $ y_1=y_2$\\
$P (0, y) \implies f(f(y))=yf(1)$ pa kad u to stavimo $y=1$ dobije se $f(f(1))=f(1)$, odnosno $f(1)=1$ zbog injektivnosti. To povlači $f(f(y))=y, \forall y$\\
Fiksirajmo $y \neq 0$. Zbog toga što je $f$ bijekcija i $y \neq 0$, postoji jedinstven $x$ takav da $f(y)=-f(xy)$. Uvrštavanjem $(x, y)$ dobiva se:
$f(x)=f(x)+yf(x+1)$, te slijedi $x=-1$ i $f(-x)=-f(x), \forall x$.\\
Konačno, za $x \neq 0$, $(x, f(-x))$:\\
$f(x+f(f(-x))+f(xf(-x)))=f(x)-f(x)f(x+1)\\
f(x)f(x+1)-xf(x)=f(x)\\
f(x+1)=x+1\\
f(x)=x$ za sve $x \neq 1$, a vrijedi i za $x=1$ pa je $f(x)=x, \forall x$
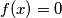 i
i 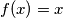 za sve realne
za sve realne  . Pretpostavimo da postoji
. Pretpostavimo da postoji  takav da
takav da 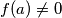 . tada uvrštavanjem
. tada uvrštavanjem 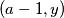 dobivamo da je f surjekcija.
dobivamo da je f surjekcija.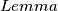 :
: 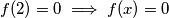 .
.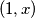 i imamo:
i imamo: 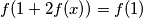 . Ali,
. Ali,  je surjektivna, pa lijeva strana može poprimiti oblik
je surjektivna, pa lijeva strana može poprimiti oblik 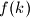 za bilo koji realni
za bilo koji realni  . Iz toga slijedi da je
. Iz toga slijedi da je  konstanta, neka je
konstanta, neka je 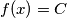 . Lagano se provjeri da može biti samo
. Lagano se provjeri da može biti samo 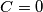 , suprotno pretpostavci.
, suprotno pretpostavci.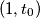 , gdje je
, gdje je 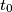 nultočka od
nultočka od  dobije se:
dobije se: 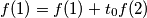 , pa je
, pa je 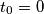
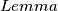 :
:  je injektivna
je injektivna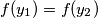 . Uvrštavanjem
. Uvrštavanjem 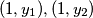 dobije se:
dobije se: 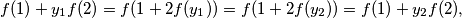 odakle
odakle 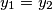
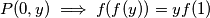 pa kad u to stavimo
pa kad u to stavimo 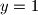 dobije se
dobije se 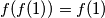 , odnosno
, odnosno 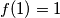 zbog injektivnosti. To povlači
zbog injektivnosti. To povlači 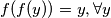
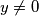 . Zbog toga što je
. Zbog toga što je  bijekcija i
bijekcija i 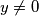 , postoji jedinstven
, postoji jedinstven  takav da
takav da 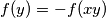 . Uvrštavanjem
. Uvrštavanjem 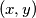 dobiva se:
dobiva se: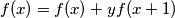 , te slijedi
, te slijedi 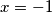 i
i 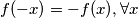 .
.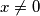 ,
, 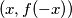 :
: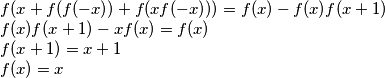 za sve
za sve 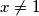 , a vrijedi i za
, a vrijedi i za  pa je
pa je 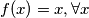
 Školjka
Školjka 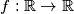 takve da
takve da 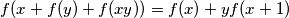 za sve
za sve 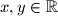 .
.