Neocijenjeno
6. kolovoza 2020. 16:01 (5 godine, 7 mjeseci)
Neka su

,

i

duljine stranica trokuta. Dokaži da tada vrijedi nejednakost:
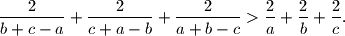
%V0
Neka su $a$, $b$ i $c$ duljine stranica trokuta. Dokaži da tada vrijedi nejednakost: $$
{2 \over b+c-a} + {2 \over c+a-b} + {2 \over a+b-c}
>{2 \over a} + {2 \over b} + {2 \over c}.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Zbog nejednakosti trokuta svi su nazivnici lijeve strane pozitivni. Koristeći lemu \(\frac{1}{1+x} = \int_0^1 t^x dt\) koja vrijedi za sve \(x > -1\), vidimo da je dana nejednakost ekvivalentna s
\[\sum_{cyc} \int_0^1 t^{b+c-a-1} dt \geq \sum_{cyc} \int_0^1 t^{a-1} dt\]
Uvedemo li supstituciju \(x = t^{a-1},y=t^{b-1},z=t^{c-1}\), dovoljno je pokazati da vrijedi \(\sum_{cyc} \frac{yz}{x} \geq \sum_{cyc} x\) za sve \(x,y,z > 0\) što slijedi iz
\[\frac{yz}{x} + \frac{xy}{z} \overset{AG}{\geq} 2y,\ \ \ \frac{xz}{y} + \frac{yz}{x} \geq 2z\ \ \ \frac{xy}{z}+\frac{xz}{y} \geq 2x\]