Točno
28. lipnja 2013. 11:14 (12 godine, 8 mjeseci)
Odredi sve funkcije
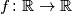
takve da je
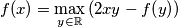
za svaki
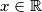
.
%V0
Odredi sve funkcije $f \colon \mathbb{R} \to \mathbb{R}$ takve da je $$ f\!\left(x\right) = \max_{y \in \mathbb{R}}{\left(2xy - f\!\left(y\right)\right)} $$ za svaki $x \in \mathbb{R}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Iz zadanog uvjeta imamo:
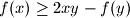
za sve
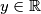
Uvrštavamo
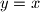
:
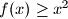
Uvodimo supstituciju
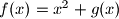
,
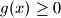
:
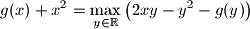
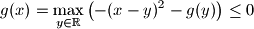
Sada imamo
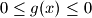
, pa je
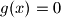
za svaki

.
Konačno,
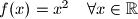
.
%V0
Iz zadanog uvjeta imamo:
$f(x) \geq 2xy - f(y)$ za sve $y \in \mathbb{R}$
Uvrštavamo $y = x$:
$f(x) \geq x^2$
Uvodimo supstituciju $f(x) = x^2 + g(x)$, $g(x) \geq 0$:
$\displaystyle g(x) + x^2 = \max_{y \in \mathbb{R}}{\left( 2xy - y^2 - g(y) \right)}$
$\displaystyle g(x) = \max_{y \in \mathbb{R}}{\left( -(x - y)^2 - g(y) \right)} \leq 0$
Sada imamo $0 \leq g(x) \leq 0$, pa je $g(x) = 0$ za svaki $x$.
Konačno, $f(x) = x^2 \quad \forall x \in \mathbb{R}$.
| 31. kolovoza 2015. 13:39 | grga | Točno |