Točno
28. lipnja 2013. 12:03 (12 godine, 8 mjeseci)
Let
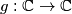
,
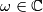
,
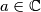
,
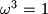
, and
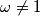
. Show that there is one and only one function
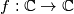
such that
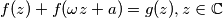
%V0
Let $g: \mathbb{C} \rightarrow \mathbb{C}$, $\omega \in \mathbb{C}$, $a \in \mathbb{C}$, $\omega^3 = 1$, and $\omega \ne 1$. Show that there is one and only one function $f: \mathbb{C} \rightarrow \mathbb{C}$ such that
$$f(z) + f(\omega z + a) = g(z),z\in \mathbb{C}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$$f(z) + f(\omega z + a) = g(z)$$ $$f(z) = g(z) - f(\omega z + a)$$ $$f(\omega z + a) = g(\omega z + a) - f(\omega^2 z + \omega a + a)$$ $$f(\omega^2 z + \omega a + a) = g(\omega^2 z + \omega a + a) - f(\omega^3 z + \omega^2 a + \omega a + a)$$
Sada imamo $\omega^3 = 1$, $\omega \neq 1$ i $1 + \omega + \omega^2 = \dfrac{1 - \omega^3}{1 - \omega} = 0$, pa je $$f(\omega^2 z + \omega a + a) = g(\omega^2 z + \omega a + a) - f(z)$$
Uvrštavamo u početnu jednadžbu:
$$f(z) + \!\left( g(\omega z + a) - \left( g(\omega^2 z + \omega a + a) - f(z) \right) \right) = g(z)$$ $$f(z) = \frac12 \left( g(z) - g(\omega z + a) + g(\omega^2 z + \omega a + a) \right)
| 31. kolovoza 2015. 13:45 | grga | Točno |