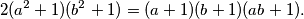Najčešći pristup nekoj zadanoj relaciji je pokušaj faktoriziranja kako bi se jednadžba pojednostavnila, no ono što je sumnjivo u ovom zadatku je to što je zadana relacija već sama po sebi "sređena". Faktorizirana je u dijelove koji se ne mogu dalje cijepati, i upravo zbog te "sređenosti" je dosta lako pronaći jedno rješenje poput 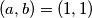 .
.
Uočimo da su nepoznanice na lijevoj strani pod kvadratima. Načelno (naravno, ne uvijek) u nejednakostima, 'individualne' varijable su puno 'jače' od 'miješanih'. Ono što time želim reći jest da ako imate neki izraz koji je suma  -tih potencija, uglavnom će on biti veći od produkta tih istih varijabli takvih da sveukupno imaju stupanj
-tih potencija, uglavnom će on biti veći od produkta tih istih varijabli takvih da sveukupno imaju stupanj  . Na primjer, vrijedi
. Na primjer, vrijedi 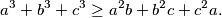
Korisno je pokušati iskoristiti neke od poznatih nejednakosti kako bismo dokazali da je lijeva strana veća ili jednaka desnoj. Tada bi nam rješenja jednadžbe proizašla iz uvjeta jednakosti svih nejednakosti koje smo koristili.
Zato je dobro imati na umu već poznato rješenje 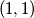 , koje ukazuje koliko "jake" nejednakosti trebamo koristiti. Primjerice najjednostavnija nejednakost kojem je
, koje ukazuje koliko "jake" nejednakosti trebamo koristiti. Primjerice najjednostavnija nejednakost kojem je 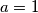 uvjet jednakosti je
uvjet jednakosti je 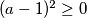 . Tu nejednakost možemo postepeno preobličavati u oblik koji se pojavljuje u zadatku na sljedeći način:
. Tu nejednakost možemo postepeno preobličavati u oblik koji se pojavljuje u zadatku na sljedeći način:
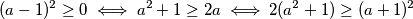 Množeći s istom nejednakosti za nepoznanicu
Množeći s istom nejednakosti za nepoznanicu  dobivamo:
dobivamo: 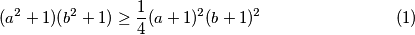
Ha, dobro  a što je s
a što je s 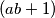 pitate se? Kako bismo
pitate se? Kako bismo 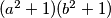 povezali s
povezali s 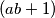 ? Srećom postoji CSB nejednakost koja je upravo ono što nam treba
? Srećom postoji CSB nejednakost koja je upravo ono što nam treba 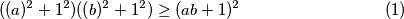
Zbrojimo li  i
i  te na njih primjenimo
te na njih primjenimo 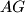 nejednakost dobivamo
nejednakost dobivamo 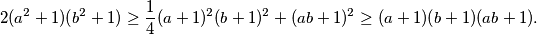
Što pokazuje je lijeva strana jednakosti veća ili jednaka od desne, potičem vas da provjerite da je slučaj jednakosti u svim nejednakostima koje smo koristili upravo riješenje 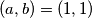 , te time da utvrdite da je
, te time da utvrdite da je 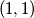 uistinu jedino riješenje jednadžbe.
uistinu jedino riješenje jednadžbe.
Naravno, postoji još jedno rješenje zadatka, potencijalno jednostavnije, no, puno manje poučno. Naime, jednadžbu možemo razmnožiti i promatrati kao kvadratnu jednadžbu u  ili u
ili u  te promatrajući diskriminantu, možemo doći do rješenja. S obzirom da je to rješenje uglavnom 'mehanički', ovdje ga neću navoditi.
te promatrajući diskriminantu, možemo doći do rješenja. S obzirom da je to rješenje uglavnom 'mehanički', ovdje ga neću navoditi.
Najčešći pristup nekoj zadanoj relaciji je pokušaj faktoriziranja kako bi se jednadžba pojednostavnila, no ono što je sumnjivo u ovom zadatku je to što je zadana relacija već sama po sebi "sređena". Faktorizirana je u dijelove koji se ne mogu dalje cijepati, i upravo zbog te "sređenosti" je dosta lako pronaći jedno rješenje poput $(a,b) = (1,1)$.
Uočimo da su nepoznanice na lijevoj strani pod kvadratima.
Načelno (naravno, ne uvijek) u nejednakostima, 'individualne' varijable su
puno 'jače' od 'miješanih'. Ono što time želim reći jest da ako imate neki
izraz koji je suma $n$-tih potencija, uglavnom će on biti veći od
produkta tih istih varijabli takvih da sveukupno imaju stupanj $n$. Na primjer,
vrijedi \[a^3 + b^3 + c^3 \geq a^2 b + b^2 c + c^2 a. \]
Korisno je pokušati iskoristiti neke od poznatih nejednakosti kako bismo dokazali da je lijeva strana veća ili jednaka desnoj. Tada bi nam rješenja jednadžbe proizašla iz uvjeta jednakosti svih nejednakosti koje smo koristili.
Zato je dobro imati na umu već poznato rješenje $(1,1)$, koje ukazuje koliko "jake" nejednakosti trebamo koristiti. Primjerice najjednostavnija nejednakost kojem je $a = 1$ uvjet jednakosti je $ (a-1)^2 \geq 0 $. Tu nejednakost možemo postepeno preobličavati u oblik koji se pojavljuje u zadatku na sljedeći način:
\[ (a-1)^2 \geq 0 \iff a^2+1 \geq 2a \iff 2(a^2+1) \geq (a+1)^2 \]
Množeći s istom nejednakosti za nepoznanicu $b$ dobivamo: \begin{equation}(a^2+1)(b^2+1) \geq \frac{1}{4}(a+1)^2(b+1)^2 \end{equation}
Ha, dobro $\cdots$ a što je s $(ab+1)$ pitate se?
Kako bismo $(a^2+1)(b^2+1)$ povezali s $(ab+1)$?
Srećom postoji CSB nejednakost koja je upravo ono što nam treba
\begin{equation} ((a)^2+1^2)((b)^2+1^2) \geq (ab+1)^2 \end{equation}
Zbrojimo li $(1)$ i $(2)$ te na njih primjenimo $AG$ nejednakost dobivamo
\[ 2(a^2+1)(b^2+1) \geq \frac{1}{4}(a+1)^2(b+1)^2 + (ab+1)^2 \geq (a+1)(b+1)(ab+1). \]
Što pokazuje je lijeva strana jednakosti veća ili jednaka od desne, potičem vas da provjerite da je slučaj jednakosti u svim nejednakostima koje smo koristili upravo riješenje $(a,b)=(1,1)$, te time da utvrdite da je $(1,1)$ uistinu jedino riješenje jednadžbe.
Naravno, postoji još jedno rješenje zadatka, potencijalno jednostavnije, no,
puno manje poučno. Naime, jednadžbu možemo razmnožiti i promatrati kao kvadratnu jednadžbu u $a$ ili u $b$ te promatrajući diskriminantu, možemo doći do rješenja. S obzirom da je
to rješenje uglavnom 'mehanički', ovdje ga neću navoditi.
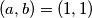 .
. -tih potencija, uglavnom će on biti veći od produkta tih istih varijabli takvih da sveukupno imaju stupanj
-tih potencija, uglavnom će on biti veći od produkta tih istih varijabli takvih da sveukupno imaju stupanj  . Na primjer, vrijedi
. Na primjer, vrijedi 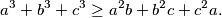
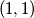 , koje ukazuje koliko "jake" nejednakosti trebamo koristiti. Primjerice najjednostavnija nejednakost kojem je
, koje ukazuje koliko "jake" nejednakosti trebamo koristiti. Primjerice najjednostavnija nejednakost kojem je 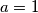 uvjet jednakosti je
uvjet jednakosti je 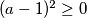 . Tu nejednakost možemo postepeno preobličavati u oblik koji se pojavljuje u zadatku na sljedeći način:
. Tu nejednakost možemo postepeno preobličavati u oblik koji se pojavljuje u zadatku na sljedeći način: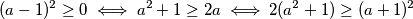 Množeći s istom nejednakosti za nepoznanicu
Množeći s istom nejednakosti za nepoznanicu  dobivamo:
dobivamo: 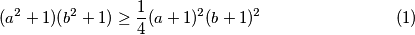
 a što je s
a što je s 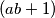 pitate se? Kako bismo
pitate se? Kako bismo 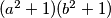 povezali s
povezali s 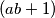 ? Srećom postoji CSB nejednakost koja je upravo ono što nam treba
? Srećom postoji CSB nejednakost koja je upravo ono što nam treba 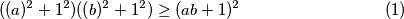
 i
i  te na njih primjenimo
te na njih primjenimo  nejednakost dobivamo
nejednakost dobivamo 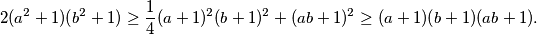
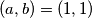 , te time da utvrdite da je
, te time da utvrdite da je 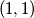 uistinu jedino riješenje jednadžbe.
uistinu jedino riješenje jednadžbe. ili u
ili u  te promatrajući diskriminantu, možemo doći do rješenja. S obzirom da je to rješenje uglavnom 'mehanički', ovdje ga neću navoditi.
te promatrajući diskriminantu, možemo doći do rješenja. S obzirom da je to rješenje uglavnom 'mehanički', ovdje ga neću navoditi.  Školjka
Školjka