Sakrij rješenje
Na kružnici je nasumično postavljeno  bijelih i
bijelih i  crnih kuglica. Počevši od proizvoljne bijele kuglice, u smjeru kazaljke na satu sve bijele kuglice su redom označene brojevima
crnih kuglica. Počevši od proizvoljne bijele kuglice, u smjeru kazaljke na satu sve bijele kuglice su redom označene brojevima 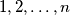 . Na isti način su i sve crne kuglice označene brojevima
. Na isti način su i sve crne kuglice označene brojevima 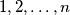 u smjeru suprotno od kazaljke na satu. Dokaži da postoji niz od
u smjeru suprotno od kazaljke na satu. Dokaži da postoji niz od  uzastopnih kuglica koje su označene brojevima
uzastopnih kuglica koje su označene brojevima 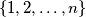 u nekom redoslijedu.
u nekom redoslijedu.
Kliknite ovdje kako biste prikazali rješenje.
Neka 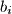 i
i 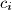 redom označavaju bijele i crne kuglice označene brojem
redom označavaju bijele i crne kuglice označene brojem  gdje je
gdje je 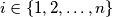
Posmatrajmo za svaki  kružni luk
kružni luk 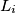 (skup), gledajući u smjeru kazaljke na satu, koji počinje "neposredno poslije
(skup), gledajući u smjeru kazaljke na satu, koji počinje "neposredno poslije 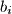 " i završava "neposredno prije
" i završava "neposredno prije 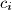 ".
".
Ako osjetite da nemate kontrolu nad elementima zadatka, pored raznih načina sistematizacije (kao što je u ovom slučaju skup 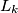 ), dosta je korisno prizvati upomoć princip ekstrema. To jest posmatrati određeni skup koji je maksimalan ili minimalan po određenom kriteriju, jer će takav skup vrlo često davati dodatna ograničenja koja se mogu pokazati korisnim. U ovom slučaju iz odabira minimalanog skupa
), dosta je korisno prizvati upomoć princip ekstrema. To jest posmatrati određeni skup koji je maksimalan ili minimalan po određenom kriteriju, jer će takav skup vrlo često davati dodatna ograničenja koja se mogu pokazati korisnim. U ovom slučaju iz odabira minimalanog skupa 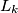 će proizaći dva niza , jedan bijeli , jedan crni čiji su skupovi indeksa disjunktni. Ajmo vidit zašto je takvo nešto korisno...
će proizaći dva niza , jedan bijeli , jedan crni čiji su skupovi indeksa disjunktni. Ajmo vidit zašto je takvo nešto korisno...
Pretpostavimo da je najmanji od kružnih lukova 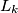 (dakle onaj koji sadrži najmanje elemenata). Sve kuglice u skupu
(dakle onaj koji sadrži najmanje elemenata). Sve kuglice u skupu 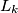 moraju biti iste boje, u protivnom bi i
moraju biti iste boje, u protivnom bi i 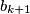 , i
, i 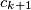 bili elementi skupa
bili elementi skupa 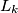 odnosno
odnosno 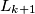 bi bio sadržan u skupu
bi bio sadržan u skupu 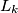 što bi se se suprotstavljalo minimalnom odabiru skupa
što bi se se suprotstavljalo minimalnom odabiru skupa 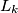 . Neka je boja elemenata u odabranom luku bez smanjenja općenitosti bijela.
. Neka je boja elemenata u odabranom luku bez smanjenja općenitosti bijela.
Ukoliko sada uzmemo kružni luk duljine  koji počinje neposredno poslije kuglice
koji počinje neposredno poslije kuglice 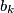 , on će sadržati bijele kuglice poredane po rastućim oznakama počevši od
, on će sadržati bijele kuglice poredane po rastućim oznakama počevši od 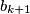 dok će crne kuglice sadržati po padajućim oznakama počevši od
dok će crne kuglice sadržati po padajućim oznakama počevši od 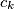 . Dakle ukoliko ima
. Dakle ukoliko ima  bijelih kuglica u disku, to će biti kuglice
bijelih kuglica u disku, to će biti kuglice 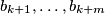 dok će crnih biti
dok će crnih biti  a to su
a to su 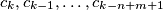 gdje sve indekse gledamo modulo
gdje sve indekse gledamo modulo  .
.
Može izgledati smješno, kako se zadatak samo "raspao". Ako malo razmislite činjenica da je najmanji 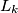 isključivo u jednoj boji (npr. bijeloj) ne dozvoljava da se
isključivo u jednoj boji (npr. bijeloj) ne dozvoljava da se 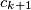 pojavi poslije
pojavi poslije 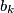 , tj. ne dozvoljava ponavljanje indeksa
, tj. ne dozvoljava ponavljanje indeksa  ,
, 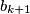 i
i 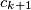 u ovom slučaju. Bez posmatranja ekstrema ne bismo mogli dobiti dva disjunkta niza indeksa koji nam trebaju da bismo upotpunili skup
u ovom slučaju. Bez posmatranja ekstrema ne bismo mogli dobiti dva disjunkta niza indeksa koji nam trebaju da bismo upotpunili skup 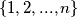 .
.
 Školjka
Školjka