Točno
22. listopada 2020. 19:06 (5 godine, 4 mjeseci)
Neka su $a$, $b$, $c$ $ \in \mathbb{R}$ takvi da vrijedi $0 \leq a$, $b$, $c \leq 1$. Dokaži nejednakost: $$a^2+b^2+c^2 \leq a^2b+b^2c+c^2a+1.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.

Uvedimo supstituciju
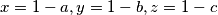
. Vrijedi
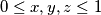
i tvrdnja postaje
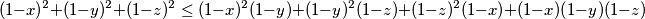
.
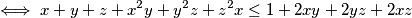
Primijetimo da vrijedi
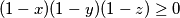
što implicira
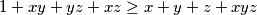
. Ako toj nejednakosti dodamo
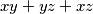
na svaku stranu, dobivamo da vrijedi
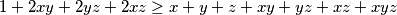
.
Ostaje nam pokazati da vrijedi
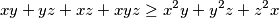
,
ali to je očito zbog
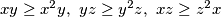
.
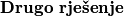
Vidimo da vrijedi
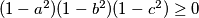
iz čega slijedi
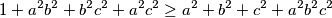
.
Dovoljno je pokazati
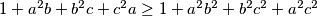
što je očito zbog
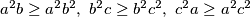
.
%V0
$\textbf{Prvo rješenje}$
Uvedimo supstituciju $x=1-a,y=1-b,z=1-c$. Vrijedi $0 \leq x,y,z \leq 1$ i tvrdnja postaje
$$(1-x)^2 + (1-y)^2+(1-z)^2 \leq (1-x)^2(1-y)+(1-y)^2(1-z)+(1-z)^2(1-x)+ (1-x)(1-y)(1-z)$$.
$$\iff x+y+z+x^2y+y^2z+z^2x\leq1+2xy+2yz+2xz$$
Primijetimo da vrijedi $(1-x)(1-y)(1-z)\geq0$ što implicira $1+xy+yz+xz\geq x+y+z+xyz$. Ako toj nejednakosti dodamo $xy+yz+xz$ na svaku stranu, dobivamo da vrijedi
$$1+2xy+2yz+2xz\geq x+y+z+xy+yz+xz+xyz$$.
Ostaje nam pokazati da vrijedi
$$xy+yz+xz+xyz\geq x^2y+y^2z+z^2x$$,
ali to je očito zbog $xy\geq x^2y,\ yz\geq y^2z,\ xz\geq z^2x$.
$\textbf{Drugo rješenje}$
Vidimo da vrijedi $(1-a^2)(1-b^2)(1-c^2)\geq 0$ iz čega slijedi
$$1+a^2b^2+b^2c^2+a^2c^2 \geq a^2+b^2+c^2+a^2b^2c^2$$.
Dovoljno je pokazati $1+a^2b+b^2c+c^2a \geq 1+a^2b^2+b^2c^2+a^2c^2$ što je očito zbog $a^2b \geq a^2b^2,\ b^2c \geq b^2c^2,\ c^2a \geq a^2c^2$.
| 22. listopada 2020. 20:06 | 11235 | Točno |
 Školjka
Školjka  ,
,  ,
, 
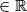 takvi da vrijedi
takvi da vrijedi 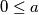 ,
, 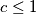 . Dokaži nejednakost:
. Dokaži nejednakost: 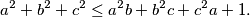

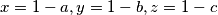 . Vrijedi
. Vrijedi 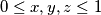 i tvrdnja postaje
i tvrdnja postaje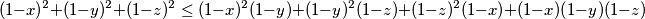 .
.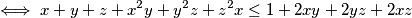
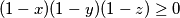 što implicira
što implicira 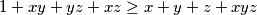 . Ako toj nejednakosti dodamo
. Ako toj nejednakosti dodamo 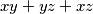 na svaku stranu, dobivamo da vrijedi
na svaku stranu, dobivamo da vrijedi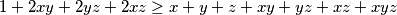 .
.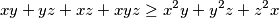 ,
,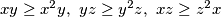 .
.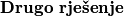
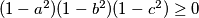 iz čega slijedi
iz čega slijedi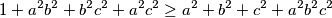 .
.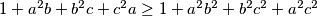 što je očito zbog
što je očito zbog 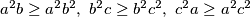 .
.