Točno
23. listopada 2020. 14:47 (5 godine, 4 mjeseci)
Postoje li $3$ prirodna broja veća od $2^{2020}$ sa svojstvom da kada umnošku bilo koja $2$ ta broja dodamo $1$ dobijemo potpuni kvadrat?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Odgovor je da, postoje takvi brojevi.
Dokazat ćemo da je 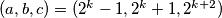 dobra trojka za svaki prirodni
dobra trojka za svaki prirodni  .
.
Zaista, imamo:
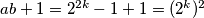
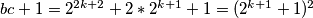
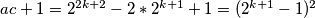 , te je zadatak riješen.
, te je zadatak riješen.
Konkretno, možemo uzeti 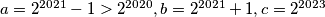
Napomena: Smatram da je najteži dio zadatka bilo pogoditi odgovor, a konstrukcija je bila motivirana malim primjerima 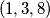 i
i 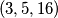
Odgovor je da, postoje takvi brojevi.\\
Dokazat ćemo da je $(a, b, c)=(2^k-1, 2^k+1, 2^{k+2})$ dobra trojka za svaki prirodni $k$.\\
Zaista, imamo:\\
$ab+1=2^{2k}-1+1=(2^k)^2$\\
$bc+1=2^{2k+2}+2*2^{k+1}+1=(2^{k+1}+1)^2$\\
$ac+1=2^{2k+2}-2*2^{k+1}+1=(2^{k+1}-1)^2$, te je zadatak riješen.
Konkretno, možemo uzeti $a=2^{2021}-1>2^{2020}, b=2^{2021}+1, c=2^{2023}$
Napomena: Smatram da je najteži dio zadatka bilo pogoditi odgovor, a konstrukcija je bila motivirana malim primjerima $(1, 3, 8)$ i $(3, 5, 16)$
 Školjka
Školjka  prirodna broja veća od
prirodna broja veća od 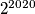 sa svojstvom da kada umnošku bilo koja
sa svojstvom da kada umnošku bilo koja  ta broja dodamo
ta broja dodamo  dobijemo potpuni kvadrat?
dobijemo potpuni kvadrat? 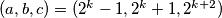 dobra trojka za svaki prirodni
dobra trojka za svaki prirodni  .
.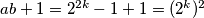
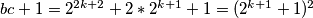
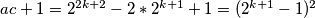 , te je zadatak riješen.
, te je zadatak riješen.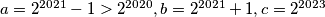
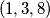 i
i