Točno
23. listopada 2020. 13:06 (5 godine, 4 mjeseci)
Odredi sumu: $$\Bigl\lfloor\dfrac{2^0}{3}\Bigr\rfloor + \Bigl\lfloor\dfrac{2^1}{3}\Bigr\rfloor + ... + \Bigl\lfloor\dfrac{2^{2020}}{3}\Bigr\rfloor$$ \\ gdje $\lfloor x \rfloor$ označava najveći cijeli broj manji od $x$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
\[S = \sum_{k=0}^{2020}\Bigl\lfloor\frac{2^k}{3}\Bigr\rfloor \]
Ispisemo prvih nekoliko elemenata.
\[ S = 0 + 0 + 1 + 2 + 5 + 10 + 21 + 42 + 85 + 170 + ... + n_{2020}\]
grupiramo
\[ S = (0 + 0) + (1 + 2) + (5 + 10) + (21 + 42) + (85 +170) + ... + (n_{2018} + n_{2019}) + n_{2020}\]
\[ \iff S =3 + 15 + 63 + 255 + ... + (n_{2018} + n_{2019}) + n_{2020} \]
\[ \iff S =(2^2 - 1) + (2^4 - 1) +(2^6 - 1)+(2^8 - 1)+...+ n_{2020} \]
\[ \iff S=(\sum_{i=1}^{1009}{4^i -1}) + \frac{4^{1010} - 1}{3} \] primjetimo sumu geometrijskoga niza
\[ \iff S = \frac{4^{1010} - 4}{3} + \frac{4^{1010} - 1}{3} - 1009 =\]
\[ = \frac{2(4^{1010} -1)}{3} - 1010 \]
\[ = \frac{2^{2021} -2 }{3} - 1010 \]
\[ 2^{2021} -2 \equiv 2 - 2 \equiv 0 \mod 3 \implies S \in \mathbb{N}\]
Rjesenje bi trebalo doraditi. Trebalo bi biti, po mom misljenju, rigoroznije.
| 23. listopada 2020. 13:11 | 11235 | Točno |
 Školjka
Školjka 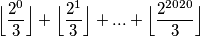
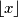 označava najveći cijeli broj manji od
označava najveći cijeli broj manji od  .
. 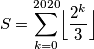
 grupiramo
grupiramo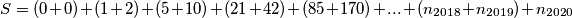
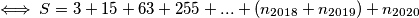

 primjetimo sumu geometrijskoga niza
primjetimo sumu geometrijskoga niza 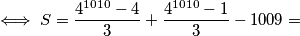
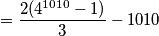
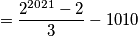
 Rjesenje bi trebalo doraditi. Trebalo bi biti, po mom misljenju, rigoroznije.
Rjesenje bi trebalo doraditi. Trebalo bi biti, po mom misljenju, rigoroznije.