Neocijenjeno
24. listopada 2020. 09:31 (5 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Tvrdimo da je odgovor da.
Promotrimo bilo koja  prirodna broja oblika
prirodna broja oblika 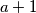 i
i  . Pokušajmo pronaći broj
. Pokušajmo pronaći broj  takav da su
takav da su 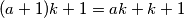 i
i 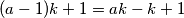 potpuni kvadrati. Ako to uspijemo tražena trojka brojeva bit će
potpuni kvadrati. Ako to uspijemo tražena trojka brojeva bit će 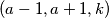 , budući da je
, budući da je 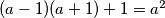 već potpun kvadrat.
već potpun kvadrat.
Namjestit ćemo da  bude srednji član u raspisu nekog kvadrata zbroja
bude srednji član u raspisu nekog kvadrata zbroja 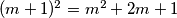 , odnosno kvadrata razlike
, odnosno kvadrata razlike 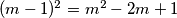 . Uzmimo da je
. Uzmimo da je  oblika
oblika 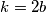 gdje je
gdje je 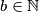 .
.
Sada nam izrazi glase 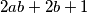 i
i 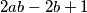 . Želimo da broj
. Želimo da broj 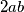 bude kvadrat pa stavimo
bude kvadrat pa stavimo 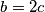 . Dakle, imamo
. Dakle, imamo 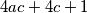 i
i 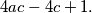 Ako još uvrstimo
Ako još uvrstimo  dobit ćemo
dobit ćemo  potpuna kvadrata
potpuna kvadrata 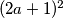 i
i 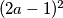 . Dakle, sve trojke oblika
. Dakle, sve trojke oblika 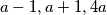 zadovoljavaju uvjet. Odaberemo li, primjerice,
zadovoljavaju uvjet. Odaberemo li, primjerice, 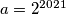 , tri broja
, tri broja 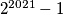 ,
, 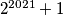 ,
, 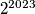 su svi veći od
su svi veći od 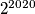 i zadovoljavaju uvjet, čime smo dokazali da takvi brojevi postoje.
i zadovoljavaju uvjet, čime smo dokazali da takvi brojevi postoje.
 Školjka
Školjka  prirodna broja veća od
prirodna broja veća od  dobijemo potpuni kvadrat?
dobijemo potpuni kvadrat?