Neocijenjeno
24. listopada 2020. 09:32 (5 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Polinom ima 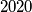 nultočaka pa ga možemo zapisati u obliku
nultočaka pa ga možemo zapisati u obliku 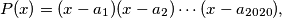 gdje su
gdje su 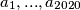 njegove nultočke.
njegove nultočke.
Vrijedi 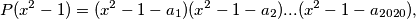 svaka zagrada u ovom polinomu je polinom koji ima ili
svaka zagrada u ovom polinomu je polinom koji ima ili  realne ili
realne ili  kompleksne nultočke.
kompleksne nultočke.
Budući da 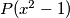 ima
ima 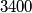 realnih nultočaka, za
realnih nultočaka, za 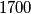 brojeva
brojeva  vrijedi
vrijedi 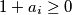 , odnosno
, odnosno 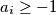 .
.
Analogno, 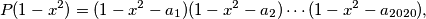 pa za barem
pa za barem 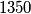 brojeva
brojeva  vrijedi
vrijedi 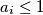 .
.
Kako  ima najviše
ima najviše 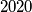 realnih nultočaka, postoji najviše
realnih nultočaka, postoji najviše 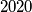 realnih brojeva
realnih brojeva 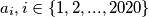 , od kojih za barem
, od kojih za barem 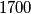 vrijedi
vrijedi 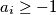 te za barem
te za barem 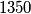 vrijedi
vrijedi 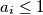 . Tada se lako dokaže da među tim brojevima postoji najmanje
. Tada se lako dokaže da među tim brojevima postoji najmanje 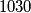 brojeva za koje vrijedi
brojeva za koje vrijedi 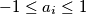 .
.
Interval ![[-1,1]](/media/m/8/d/9/8d92f93662539c83dd14147b1aec5197.png) možemo podijeliti u
možemo podijeliti u 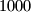 jednakih podintervala, razlika bilo koja
jednakih podintervala, razlika bilo koja  elementa u nekom podintervalima je
elementa u nekom podintervalima je 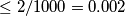 , a po Dirichletovom principu znamo da barem
, a po Dirichletovom principu znamo da barem  nultočke leže u istom podintervalu.
nultočke leže u istom podintervalu.
 Školjka
Školjka 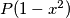 ima
ima 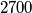 realnih nultočaka, dokaži da onda postoje dvije realne nultočke od
realnih nultočaka, dokaži da onda postoje dvije realne nultočke od 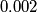 .
.