Neocijenjeno
24. listopada 2020. 09:33 (5 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Kako bi zadani izraz bio prirodan broj, broj 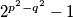 mora biti prirodan pa je i
mora biti prirodan pa je i  .
.
Budući da je tada 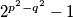 neparan,
neparan,  i
i  moraju biti različiti od
moraju biti različiti od  .
.
Sada, budući da su  i
i  različiti i neparni, vrijedi
različiti i neparni, vrijedi 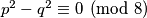 . Isto tako, ako je
. Isto tako, ako je 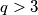 , vrijedi
, vrijedi 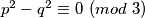 , pa sada možemo pisati
, pa sada možemo pisati 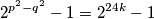 Broj
Broj 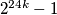 djeljiv je sa
djeljiv je sa 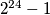 , što je djeljivo sa
, što je djeljivo sa 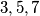 i
i  pa očito vrijedi
pa očito vrijedi 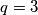 .
.
Sada želimo da 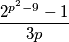 bude umnožak točno
bude umnožak točno  prosta broja.
prosta broja.
Budući da je 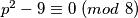 , zapišemo početni izraz kao:
, zapišemo početni izraz kao: 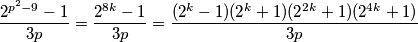
Lagano je provjeriti da je 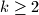 . Ako je
. Ako je  paran, onda
paran, onda 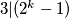 i ako je
i ako je 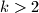 , onda je
, onda je 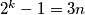 za neki prirodan broj
za neki prirodan broj 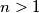 , ali onda je
, ali onda je 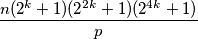 umnožak barem
umnožak barem  prosta broja što je u kontradikciji s pretpostavkom.
prosta broja što je u kontradikciji s pretpostavkom.
Za 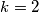 dobivamo
dobivamo 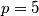 , što zadovoljava uvjet zadatka.
, što zadovoljava uvjet zadatka.
Ako je  neparan, vrijedi
neparan, vrijedi 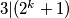 pa je
pa je 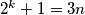 za neki prirodan broj
za neki prirodan broj 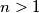 , no onda je
, no onda je 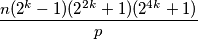 ponovno umnožak barem
ponovno umnožak barem  prosta broja.
prosta broja.
Dakle, jedino rješenje je 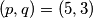 .
.
 Školjka
Školjka 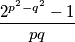 umnožak točno
umnožak točno