Sakrij rješenje
Neka je  prirodan broj veći od
prirodan broj veći od  . Na kružnici je
. Na kružnici je 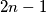 jednako udaljenih točaka od kojih je točno
jednako udaljenih točaka od kojih je točno  obojano crveno. Takvo bojanje zovemo
obojano crveno. Takvo bojanje zovemo 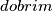 ako postoji barem jedan par crvenih točaka takvih da se unutar jednog luka koji taj par tvori nalazi točno
ako postoji barem jedan par crvenih točaka takvih da se unutar jednog luka koji taj par tvori nalazi točno  točaka. Odredi najmanji mogući
točaka. Odredi najmanji mogući  za koji je svako bojanje točaka na kružnici
za koji je svako bojanje točaka na kružnici 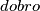 .
.
Kliknite ovdje kako biste prikazali rješenje.
Umjesto dobrih gledat ćemo loša bojanja koja definiramo kao sva bojanja koja nisu dobra.
Neka je  maksimalan broj točaka koje loše bojanje može imati. Dakle
maksimalan broj točaka koje loše bojanje može imati. Dakle 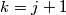 tj. tražimo
tj. tražimo  .
.
Označit ćemo vrhove sa 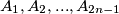 . Spojimo svaki par
. Spojimo svaki par 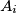 i
i 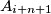 promatrajući indekse modulo
promatrajući indekse modulo 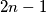 . Bojanje je loše ako i samo ako su
. Bojanje je loše ako i samo ako su  crvena vrha spojena tetivom. Ako se krenemo tetivama "kretati" u jednom smjeru iz vrha u vrh te se u nekom trenutku vratimo na isti vrh to zovemo ciklusom. Tih ciklusa u ovom slučaju ima
crvena vrha spojena tetivom. Ako se krenemo tetivama "kretati" u jednom smjeru iz vrha u vrh te se u nekom trenutku vratimo na isti vrh to zovemo ciklusom. Tih ciklusa u ovom slučaju ima 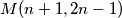 , gdje
, gdje 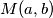 predstavlja najveći zajednički djelitelj brojeva
predstavlja najveći zajednički djelitelj brojeva  i
i  .
.
Primjenom Euklidovog algoritma dobivamo da je 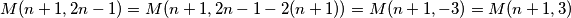 Dakle ako je
Dakle ako je  djeljivo s
djeljivo s  , onda je
, onda je  ciklusa, inače je samo
ciklusa, inače je samo  . Ako je samo
. Ako je samo  ciklus očito je
ciklus očito je 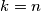 .
.
Ako je pak  ciklusa koji svaki sadrži
ciklusa koji svaki sadrži 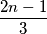 vrha, svaki ciklus može imati maksimalno
vrha, svaki ciklus može imati maksimalno 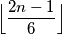 crvenih točaka u lošem bojanju.
crvenih točaka u lošem bojanju.
Dakle, u ovom slučaju 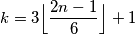
 Školjka
Školjka