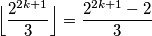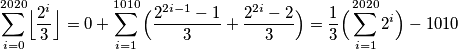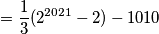Neocijenjeno
24. listopada 2020. 09:38 (5 godine, 4 mjeseci)
Sakrij rješenje
Odredi sumu: $$\Bigl\lfloor\dfrac{2^0}{3}\Bigr\rfloor + \Bigl\lfloor\dfrac{2^1}{3}\Bigr\rfloor + ... + \Bigl\lfloor\dfrac{2^{2020}}{3}\Bigr\rfloor$$ \\ gdje $\lfloor x \rfloor$ označava najveći cijeli broj manji od $x$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Pokušat ćemo svaki izraz $\Bigl\lfloor\dfrac{2^n}{3}\Bigr\rfloor$ zapisati kao razlomak bez neugodnih zagrada, takvim postupkom bi nam se neke varijable mogle pokratiti. Primijetimo da: $$ 2^{2k} \equiv 1 \pmod{3} $$
$$2^{2k+1} \equiv 2 \pmod{3}$$
Ovo znači da $\Bigl\lfloor\dfrac{2^{2k}}{3}\Bigr\rfloor = \dfrac{2^{2k}-1}{3}$ i $\Bigl\lfloor\dfrac{2^{2k+1}}{3}\Bigr\rfloor = \dfrac{2^{2k+1}-2}{3}$ \\
\\
Naša suma se zapravo pretvara u
$$ \sum_{i=0}^{2020} \Bigl\lfloor\dfrac{2^i}{3}\Bigr\rfloor = 0 + \sum_{i=1}^{1010} \Big{(} \dfrac{2^{2i-1}-1}{3} + \dfrac{2^{2i}-2}{3} \Big{)} = \dfrac{1}{3} \Big{(} \sum_{i=1}^{2020} 2^{i}\Big{)} -1010$$ $$ = \dfrac{1}{3}(2^{2021}-2)-1010$$
 Školjka
Školjka 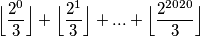
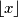 označava najveći cijeli broj manji od
označava najveći cijeli broj manji od  .
. 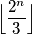 zapisati kao razlomak bez neugodnih zagrada, takvim postupkom bi nam se neke varijable mogle pokratiti. Primijetimo da:
zapisati kao razlomak bez neugodnih zagrada, takvim postupkom bi nam se neke varijable mogle pokratiti. Primijetimo da: 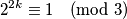
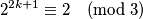
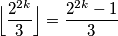 i
i