Neocijenjeno
24. listopada 2020. 09:38 (5 godine, 4 mjeseci)
Sakrij rješenje
Neka su $a$, $b$, $c$ $ \in \mathbb{R}$ takvi da vrijedi $0 \leq a$, $b$, $c \leq 1$. Dokaži nejednakost: $$a^2+b^2+c^2 \leq a^2b+b^2c+c^2a+1.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Naša nejednakost je ekvivalentna s $$a^2(1-b)+b^2(1-c)+c^2(1-a) \leq 1$$
Iskoristimo uvjet $a \leq 1$ tj. $a^2 \leq a$, pa sada imamo: $$a^2(1-b)+b^2(1-c)+c^2(1-a) \leq a(1-b)+b(1-c)+c(1-a) $$
Primijetimo sada da:
\begin{align*}
a(1-b)+b(1-c)+c(1-a)&=a+b+c-ab-bc-ac\\
&=1-(1-a-b-c+ab+bc+ac-abc)-abc\\
&=1-(1-a)(1-b)(1-c)-abc.
\end{align*}
Zbog toga što vrijedi $1-a \geq 0$ i $abc \geq 0$ slijedi $$1-(1-a)(1-b)(1-c)-abc \leq 1$$
čime smo dokazali nejednakost. \\ \\
Bitno je primijetiti da se jednakost postiže za $a=b=1$ i $c=0$.
 Školjka
Školjka  ,
,  ,
, 
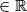 takvi da vrijedi
takvi da vrijedi 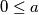 ,
, 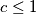 . Dokaži nejednakost:
. Dokaži nejednakost: 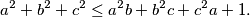
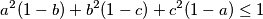 Iskoristimo uvjet
Iskoristimo uvjet 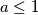 tj.
tj. 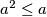 , pa sada imamo:
, pa sada imamo: 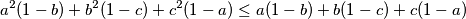 Primijetimo sada da:
Primijetimo sada da: 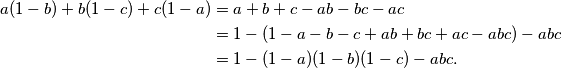 Zbog toga što vrijedi
Zbog toga što vrijedi 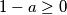 i
i 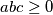 slijedi
slijedi 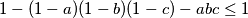 čime smo dokazali nejednakost.
čime smo dokazali nejednakost. 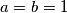 i
i 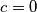 .
.