Sakrij rješenje
Zadatak: 2. lakša simulacija državnog natjecanja 2020. zadatak 3 (Sakrij tekst zadatka)
Kliknite ovdje kako biste prikazali rješenje.
Jasno je da svaki skup koji sadrži  broja koji svi daju isti ostatak pri dijeljenju s
broja koji svi daju isti ostatak pri dijeljenju s  zadovoljava svojstvo.
zadovoljava svojstvo.
Također je jasno da svaki skup u kojem postoje  broja
broja 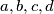 takva da
takva da  i
i  daju isti ostatak pri dijeljenju s
daju isti ostatak pri dijeljenju s  , i
, i  i
i  daju isti ostatak pri dijeljenju s
daju isti ostatak pri dijeljenju s  , zadovoljava svojstvo.
, zadovoljava svojstvo.
Promotrimo  brojeva koji svi daju različite ostatke pri dijeljenju s
brojeva koji svi daju različite ostatke pri dijeljenju s  . Od njih možemo napraviti
. Od njih možemo napraviti 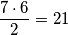 par. Zbrojimo li prvi i drugi član para u svim parovima, jasno je da ćemo dobiti
par. Zbrojimo li prvi i drugi član para u svim parovima, jasno je da ćemo dobiti 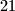 zbroj. Po Dirichletovom principu zato slijedi barem
zbroj. Po Dirichletovom principu zato slijedi barem  zbroja imaju isti ostatak pri dijeljenju s
zbroja imaju isti ostatak pri dijeljenju s  .
.
Dokažimo da se u ta  para ne nalazi isti broj. Pretpostavimo suprotno: neka su
para ne nalazi isti broj. Pretpostavimo suprotno: neka su  i
i 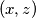 parovi čiji zbrojevi daju isti ostatak pri dijeljenju s
parovi čiji zbrojevi daju isti ostatak pri dijeljenju s  . Vrijedi
. Vrijedi 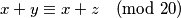 odnosno
odnosno 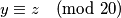 što je u kontradikciji s pretpostavkom da tih
što je u kontradikciji s pretpostavkom da tih  brojeva svi daju međusobno različite ostatke pri dijeljenju s
brojeva svi daju međusobno različite ostatke pri dijeljenju s  .
.
Zaključujemo da u svakom skupu koji sadrži  brojeva koji daju različite ostatke modulo
brojeva koji daju različite ostatke modulo  sigurno postoje barem 2 para
sigurno postoje barem 2 para 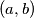 i
i 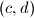 tako da vrijedi
tako da vrijedi 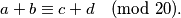 Drugim riječima, takav skup zadovoljava svojstvo.
Drugim riječima, takav skup zadovoljava svojstvo.
Pronađimo najmanji  takav da skup
takav da skup  cijelih brojeva nužno zadovoljava svojstvo. To vrijedi za
cijelih brojeva nužno zadovoljava svojstvo. To vrijedi za 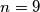 , jer ako postoji
, jer ako postoji  brojeva koji svi daju različiti ostatak pri dijeljenju s
brojeva koji svi daju različiti ostatak pri dijeljenju s  , gotovi smo. Inače u skupu imamo najviše
, gotovi smo. Inače u skupu imamo najviše  različitih ostataka modulo
različitih ostataka modulo  .
.
Imamo  slučaja:
slučaja: ![\begin{itemize}
\item[$1^{\circ}$] Postoje neka 2 ostatka pri dijeljenju sa $20$ koja se oba pojavljuju više od jednom pa smo gotovi.
\item[$2^{\circ}$] Neki se ostatak pojavljuje najmanje $4$ puta, pa smo gotovi.
\end{itemize}](/media/m/c/0/4/c04b3a2bbd856e89966a217547ea7e01.png)
Dokazali smo da svaki skup cijelih brojeva sa  članova zadovoljava svojstvo.
članova zadovoljava svojstvo.
Sada je lagano za 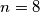 konstruirati protuprimjer
konstruirati protuprimjer 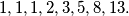
 Školjka
Školjka 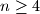 takav da za svaki skup
takav da za svaki skup  koji sadrži točno
koji sadrži točno 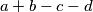 djeljiv s
djeljiv s