Neocijenjeno
24. listopada 2020. 09:40 (5 godine, 4 mjeseci)
Sakrij rješenje
Dan je paralelogram $ABCD$ i u njemu točka $X$ tako da vrijedi $|\angle AXB| + |\angle CXD| = 180^\circ$. Odredi vrijednost izraza: $$ |\angle XAB| + |\angle XDC| + |\angle CXB|.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Docrtajmo točku $X'$ t.d. je $XBCX'$ isto tako paralelogram.
\\ Sada primijetimo da je onda i $AXX'D$ paralelogram, pa vrijedi $|DX'| = |AX|$, $|CX'|=|BX|$ i $|DC|=|AB|$, pa slijedi $$ \triangle AXB \cong \triangle DX'C .$$
Sada vidimo da vrijedi $$ \angle DX'C+ \angle DXC = \angle AXB + \angle DXC = 180^{\circ}, $$ dakle $DXX'C$ je tetivan četverokut.
Koristeći tetivnost i paralelogram $XBCX'$ dobivamo $$\angle XDC = \angle XX'C = \angle XBC\ i \ \angle XAC = \angle X'DC = \angle XCB.$$
Iz ovoga zaključujemo da je suma početnih kuteva $180^{\circ}$.
 Školjka
Školjka  i u njemu točka
i u njemu točka  tako da vrijedi
tako da vrijedi 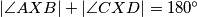 . Odredi vrijednost izraza:
. Odredi vrijednost izraza: 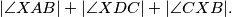
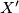 t.d. je
t.d. je 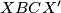 isto tako paralelogram.
isto tako paralelogram. 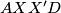 paralelogram, pa vrijedi
paralelogram, pa vrijedi 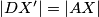 ,
, 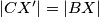 i
i 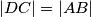 , pa slijedi
, pa slijedi 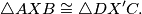
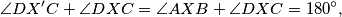 dakle
dakle 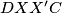 je tetivan četverokut.
je tetivan četverokut.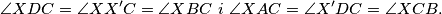 Iz ovoga zaključujemo da je suma početnih kuteva
Iz ovoga zaključujemo da je suma početnih kuteva 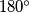 .
.