Školjka

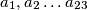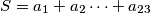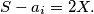Označimo s $a_1,a_2\dots a_{23}$ težine osoba i $S=a_1+a_2\dots+a_{23}$. Uvjet zadatka nam govori da ako maknemo osobu sa težinom $a_i$, ostatak možemo staviti u dvije ekipe težine $X$. Stoga $$S-a_i=2X.$$ To nam govori da $S$ i $a_i$ imaju istu parnost. Budući da ovo možemo napraviti za svaki $i$, slijedi da su ili svi $a_i$ parni, ili svi neparni. Napravit ćemo niz 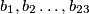$b_1, b_2\dots, b_{23}$ novih težina koji zadovoljava uvjete zadatka. \begin{itemize} \item[$1^{\circ}$] Ako su $a_i$ parni uzmimo $b_i=\frac{a_i}{2}$. \item[$2^{\circ}$] Ako su neparni $b_i=a_{i}-1$. \end{itemize} Očito novi niz zadovoljava uvjete zadatka i 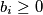$b_i\geq0$ za sve $i$. 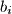Ako svi $a_i$ nisu $0$ suma $b_i$ je strogo manja od sume $a_i$. Ako nastavimo ponavljati postupak, u svakom koraku suma težina se smanjuje pa ćemo u jednom trenutku dobiti niz koji se sastoji samo od nula. Kako ovo možemo napraviti, zaključujemo da su sve težine na početku bile jednake, jer su i na kraju jednake, a ova transformacija čuva jednakost brojeva.