Školjka

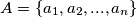Neka je $A=\{a_1,a_2,...,a_n\}$ skup koji zadovoljava uvjet.\\ \\ Označimo sa 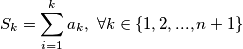\[ S_k = \sum_{i=1}^{k} a_k ,\ \forall k \in \{1,2,...,n+1\} \] Primijetimo da svaki 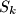$S_k$ daje različiti ostatak pri dijeljenju s $n+1$ jer u suprotnom bi imali 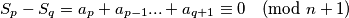$$S_p - S_q = a_p + a_{p-1}... + a_{q+1} \equiv 0 \pmod{n+1}$$ što je suprotno početnoj pretpostavci zadatka. Gledajmo sada izraz 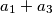$a_1+a_3$, on ima isti ostatak kao neki od 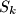$S_k$-ova. 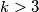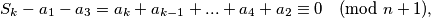Ako je $k>3$ onda $$S_k-a_1-a_3 = a_k+a_{k-1}+...+a_4+a_2 \equiv 0 \pmod{n+1},$$ što nije moguće. Ako je 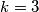$k=3$ onda je 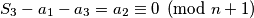$S_3-a_1-a_3 = a_2 \equiv 0 \pmod{n+1}$, što je isto nemoguće. Ako je 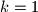$k=1$ onda je 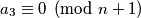$a_3 \equiv 0 \pmod{n+1}$, što je nemoguće. Preostaje samo 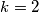$k=2$ što nam daje 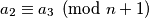$a_2 \equiv a_3 \pmod{n+1}$. Budući da smo nasumično odabrali redoslijed elemenata u $A$ slijedi da svi elementi iz $A$ daju isti ostatak pri dijeljenju sa $n+1$. 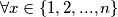Neka je taj ostatak $k$, onda on $\forall x \in \{1,2,...,n\}$ ne smije zadovoljavati jednadžbu 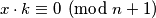$x\cdot k \equiv 0 \pmod{n+1}$, što vrijedi ako i samo ako je $k$ relativno prost s $n+1$. Dakle, svaki skup koji je rješenje je oblika 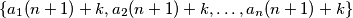$\{a_1(n+1)+k, a_2(n+1)+k, \ldots, a_n(n+1)+k\}$, gdje je $k$ prirodan broj relativno prost s $n+1$, a $a_i$ su neki različiti prirodni brojevi.