Uvrštavanjem vidimo da 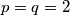 nije rješenje i da je
nije rješenje i da je 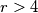 . Pretpostavimo da su i
. Pretpostavimo da su i  i
i  neparni: tada je
neparni: tada je 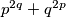 parno, odnosno
parno, odnosno  je paran prost broj veći od 4 - kontradikcija.
je paran prost broj veći od 4 - kontradikcija.
Znači da je ili  ili
ili  paran, ali s obzirom da su oba broja prosta i znamo da
paran, ali s obzirom da su oba broja prosta i znamo da 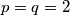 nije rješenje, točno jedan od ta dva broja je jednak 2. Bez smanjenja općenitosti, neka je
nije rješenje, točno jedan od ta dva broja je jednak 2. Bez smanjenja općenitosti, neka je 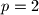 jer je jednadžba simetrična po pitanju
jer je jednadžba simetrična po pitanju  i
i  (ako je (
(ako je (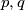 ) rješenje onda je i (
) rješenje onda je i (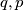 )). Početna jednadžba onda postaje
)). Početna jednadžba onda postaje 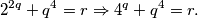 Zadatku možemo dalje pristupiti na dva načina:
Zadatku možemo dalje pristupiti na dva načina:
1. NAČIN
Promotrimo ovaj izraz modulo 5. 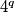 daje ostatak
daje ostatak  ili
ili 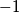 pri djeljenju s 5, ovisno o parnosti broja
pri djeljenju s 5, ovisno o parnosti broja  (-1 ako je
(-1 ako je  neparan, a
neparan, a  ako je
ako je  paran). Kako smo zaključili da je
paran). Kako smo zaključili da je  neparan, znači da
neparan, znači da 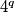 daje ostatak
daje ostatak 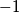 pri dijeljenju s 5. S druge strane,
pri dijeljenju s 5. S druge strane, 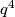 daje ostatak 1 ili 0 pri dijeljenju s 5. Sada razlikujemo dva slučaja:
daje ostatak 1 ili 0 pri dijeljenju s 5. Sada razlikujemo dva slučaja:
1. slučaj: 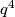 je djeljiv s
je djeljiv s  .
.
Kako je  prost broj, a
prost broj, a 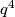 je djeljivo s 5 ako i samo ako je
je djeljivo s 5 ako i samo ako je  djeljiv s 5, jedina mogućnost je
djeljiv s 5, jedina mogućnost je 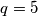 . Preostaje provjeriti je li
. Preostaje provjeriti je li 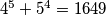 prost broj. Kako je
prost broj. Kako je 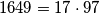 , ovaj slučaj nema rješenja.
, ovaj slučaj nema rješenja.
2. slučaj: 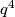 daje ostatak 1 pri djeljenju s
daje ostatak 1 pri djeljenju s  .
.
Kako 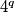 daje ostatak
daje ostatak 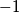 pri djeljenju s
pri djeljenju s  ,
, 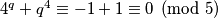 , odnosno
, odnosno  je djeljiv s 5. Kako je
je djeljiv s 5. Kako je  prost broj,
prost broj, 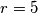 je jedina mogućnost. Međutim, jednadžba
je jedina mogućnost. Međutim, jednadžba 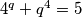 nema rješenje u prostim brojevima jer
nema rješenje u prostim brojevima jer 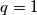 nije prost broj.
nije prost broj.
Zaključujemo da ne postoje prosti brojevi 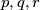 takvi da je
takvi da je 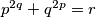 .
.
2. NAČIN
Možemo koristiti identitet Sophie Germain, koji nam daje faktorizaciju 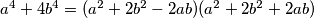 . Znamo da je
. Znamo da je  neparan i veći ili jednak 3, pa ga možemo zapisati kao
neparan i veći ili jednak 3, pa ga možemo zapisati kao 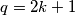 ,
, 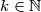 . Dalje, ako promotrimo
. Dalje, ako promotrimo 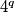 , možemo ga raspisati kao:
, možemo ga raspisati kao: 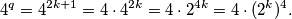 Sada je naš početni izraz postao
Sada je naš početni izraz postao 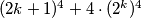 , na što možemo primijeniti prije spomenut identitet:
, na što možemo primijeniti prije spomenut identitet: 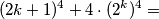
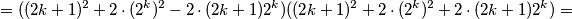
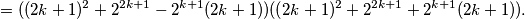
Preostaje dokazati da je svaka od ovih zagrada veća od 1. Za 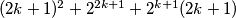 je to očito jer su svi članovi pozitivni i veći od 1. S druge strane, za
je to očito jer su svi članovi pozitivni i veći od 1. S druge strane, za 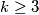 vrijedi
vrijedi 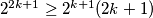 (dokaz ostavljamo vama za vježbu - indukcija ili nešto drugo...) pa je
(dokaz ostavljamo vama za vježbu - indukcija ili nešto drugo...) pa je 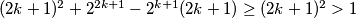 . Preostaje još provjera za
. Preostaje još provjera za 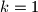 i
i 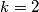 (isto ostavljamo vama - samo uvrštavanje...)
(isto ostavljamo vama - samo uvrštavanje...)
Dobili smo da je 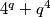 uvijek složen broj pa ova jednadžba nema rješenja za
uvijek složen broj pa ova jednadžba nema rješenja za 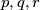 proste.
proste.
Uvrštavanjem vidimo da $p=q=2$ nije rješenje i da je $r > 4$. Pretpostavimo da su i $p$ i $q$ neparni: tada je $p^{2q}+q^{2p}$ parno, odnosno $r$ je paran prost broj veći od 4 - kontradikcija.\\
Znači da je ili $p$ ili $q$ paran, ali s obzirom da su oba broja prosta i znamo da $p=q=2$ nije rješenje, točno jedan od ta dva broja je jednak 2. Bez smanjenja općenitosti, neka je $p=2$ jer je jednadžba simetrična po pitanju $p$ i $q$ (ako je ($p, q$) rješenje onda je i ($q, p$)). Početna jednadžba onda postaje \[ 2^{2q} + q^{4}=r \Rightarrow 4^q+q^4=r. \]
Zadatku možemo dalje pristupiti na dva načina: \\
1. NAČIN \\
Promotrimo ovaj izraz modulo 5. $4^q$ daje ostatak $1$ ili $-1$ pri djeljenju s 5, ovisno o parnosti broja $q$ (-1 ako je $q$ neparan, a $1$ ako je $q$ paran). Kako smo zaključili da je $q$ neparan, znači da $4^q$ daje ostatak $-1$ pri dijeljenju s 5. S druge strane, $q^4$ daje ostatak 1 ili 0 pri dijeljenju s 5. Sada razlikujemo dva slučaja: \\
1. slučaj: $q^4$ je djeljiv s $5$. \\
Kako je $q$ prost broj, a $q^4$ je djeljivo s 5 ako i samo ako je $q$ djeljiv s 5, jedina mogućnost je $q=5$. Preostaje provjeriti je li $4^5+5^4=1649$ prost broj. Kako je $1649=17\cdot 97$, ovaj slučaj nema rješenja. \\
2. slučaj: $q^4$ daje ostatak 1 pri djeljenju s $5$.\\
Kako $4^q$ daje ostatak $-1$ pri djeljenju s $5$, $4^q+q^4 \equiv -1+1 \equiv 0 \pmod{5}$, odnosno $r$ je djeljiv s 5. Kako je $r$ prost broj, $r=5$ je jedina mogućnost. Međutim, jednadžba $4^q+q^4=5$ nema rješenje u prostim brojevima jer $q=1$ nije prost broj. \\
Zaključujemo da ne postoje prosti brojevi $p, q, r$ takvi da je $p^{2q}+q^{2p}=r$.\\
2. NAČIN \\
Možemo koristiti identitet Sophie Germain, koji nam daje faktorizaciju $a^4+4b^4=(a^2+2b^2-2ab)(a^2+2b^2+2ab)$. Znamo da je $q$ neparan i veći ili jednak 3, pa ga možemo zapisati kao $q=2k+1$, $k \in \mathbb{N}$. Dalje, ako promotrimo $4^q$, možemo ga raspisati kao: $$ 4^q=4^{2k+1}=4\cdot 4^{2k}=4\cdot 2^{4k}=4 \cdot (2^k)^4. $$
Sada je naš početni izraz postao $(2k+1)^4+4\cdot (2^k)^4$, na što možemo primijeniti prije spomenut identitet:
$$ (2k+1)^4+4\cdot (2^k)^4=$$
$$=((2k+1)^2+2\cdot (2^k)^2-2\cdot(2k+1)2^k) ((2k+1)^2+2\cdot (2^k)^2+2\cdot(2k+1)2^k)= $$
$$=((2k+1)^2+2^{2k+1}-2^{k+1}(2k+1))((2k+1)^2+2^{2k+1}+2^{k+1}(2k+1)). $$
\\
Preostaje dokazati da je svaka od ovih zagrada veća od 1. Za $(2k+1)^2+2^{2k+1}+2^{k+1}(2k+1)$ je to očito jer su svi članovi pozitivni i veći od 1. S druge strane, za $k \geq 3$ vrijedi $2^{2k+1} \geq 2^{k+1}(2k+1)$ (dokaz ostavljamo vama za vježbu - indukcija ili nešto drugo...) pa je $(2k+1)^2+2^{2k+1}-2^{k+1}(2k+1) \geq (2k+1)^2 > 1$. Preostaje još provjera za $k=1$ i $k=2$ (isto ostavljamo vama - samo uvrštavanje...) \\
Dobili smo da je $4^q+q^4$ uvijek složen broj pa ova jednadžba nema rješenja za $p, q, r$ proste.
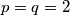 nije rješenje i da je
nije rješenje i da je 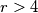 . Pretpostavimo da su i
. Pretpostavimo da su i  i
i  neparni: tada je
neparni: tada je 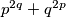 parno, odnosno
parno, odnosno  je paran prost broj veći od 4 - kontradikcija.
je paran prost broj veći od 4 - kontradikcija. ili
ili  paran, ali s obzirom da su oba broja prosta i znamo da
paran, ali s obzirom da su oba broja prosta i znamo da 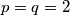 nije rješenje, točno jedan od ta dva broja je jednak 2. Bez smanjenja općenitosti, neka je
nije rješenje, točno jedan od ta dva broja je jednak 2. Bez smanjenja općenitosti, neka je 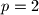 jer je jednadžba simetrična po pitanju
jer je jednadžba simetrična po pitanju  i
i  (ako je (
(ako je (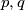 ) rješenje onda je i (
) rješenje onda je i (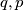 )). Početna jednadžba onda postaje
)). Početna jednadžba onda postaje 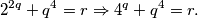 Zadatku možemo dalje pristupiti na dva načina:
Zadatku možemo dalje pristupiti na dva načina: 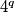 daje ostatak
daje ostatak  ili
ili 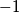 pri djeljenju s 5, ovisno o parnosti broja
pri djeljenju s 5, ovisno o parnosti broja  (-1 ako je
(-1 ako je  neparan, a
neparan, a  ako je
ako je  paran). Kako smo zaključili da je
paran). Kako smo zaključili da je  neparan, znači da
neparan, znači da 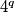 daje ostatak
daje ostatak 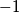 pri dijeljenju s 5. S druge strane,
pri dijeljenju s 5. S druge strane, 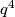 daje ostatak 1 ili 0 pri dijeljenju s 5. Sada razlikujemo dva slučaja:
daje ostatak 1 ili 0 pri dijeljenju s 5. Sada razlikujemo dva slučaja: 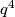 je djeljiv s
je djeljiv s  .
.  prost broj, a
prost broj, a 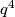 je djeljivo s 5 ako i samo ako je
je djeljivo s 5 ako i samo ako je  djeljiv s 5, jedina mogućnost je
djeljiv s 5, jedina mogućnost je 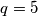 . Preostaje provjeriti je li
. Preostaje provjeriti je li 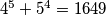 prost broj. Kako je
prost broj. Kako je 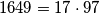 , ovaj slučaj nema rješenja.
, ovaj slučaj nema rješenja. 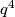 daje ostatak 1 pri djeljenju s
daje ostatak 1 pri djeljenju s  .
.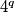 daje ostatak
daje ostatak 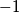 pri djeljenju s
pri djeljenju s  ,
, 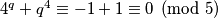 , odnosno
, odnosno  je djeljiv s 5. Kako je
je djeljiv s 5. Kako je  prost broj,
prost broj, 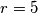 je jedina mogućnost. Međutim, jednadžba
je jedina mogućnost. Međutim, jednadžba 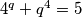 nema rješenje u prostim brojevima jer
nema rješenje u prostim brojevima jer 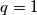 nije prost broj.
nije prost broj.  takvi da je
takvi da je 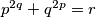 .
.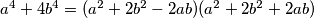 . Znamo da je
. Znamo da je  neparan i veći ili jednak 3, pa ga možemo zapisati kao
neparan i veći ili jednak 3, pa ga možemo zapisati kao 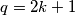 ,
, 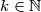 . Dalje, ako promotrimo
. Dalje, ako promotrimo 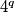 , možemo ga raspisati kao:
, možemo ga raspisati kao: 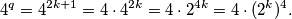 Sada je naš početni izraz postao
Sada je naš početni izraz postao 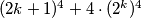 , na što možemo primijeniti prije spomenut identitet:
, na što možemo primijeniti prije spomenut identitet: 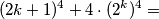
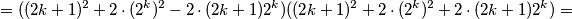
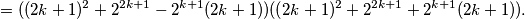
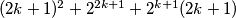 je to očito jer su svi članovi pozitivni i veći od 1. S druge strane, za
je to očito jer su svi članovi pozitivni i veći od 1. S druge strane, za 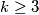 vrijedi
vrijedi 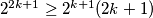 (dokaz ostavljamo vama za vježbu - indukcija ili nešto drugo...) pa je
(dokaz ostavljamo vama za vježbu - indukcija ili nešto drugo...) pa je 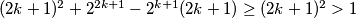 . Preostaje još provjera za
. Preostaje još provjera za 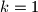 i
i 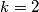 (isto ostavljamo vama - samo uvrštavanje...)
(isto ostavljamo vama - samo uvrštavanje...) 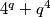 uvijek složen broj pa ova jednadžba nema rješenja za
uvijek složen broj pa ova jednadžba nema rješenja za 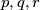 proste.
proste.  Školjka
Školjka