Točno
25. listopada 2020. 19:19 (5 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Koristeći Vieteove formule dobivamo da je dovoljno pokazati da su izrazi 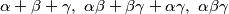 cijeli brojevi.
cijeli brojevi.
Uvedimo supstituciju 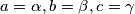 .
.
Označimo 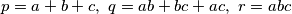
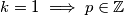
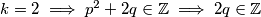 , pa je
, pa je 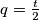 ,
, 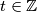
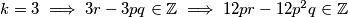
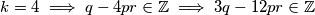
Zbrajanjem zadnja  izraza dobivamo
izraza dobivamo 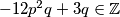 tj.
tj. 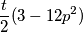 je cijeli broj. Budući da je
je cijeli broj. Budući da je 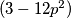 uvijek neparan,
uvijek neparan,  mora biti uvijek paran, odnosno
mora biti uvijek paran, odnosno 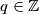 .
.
Sada još trebamo pokazati 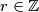 .
.
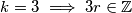 , pa je
, pa je 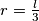 ,
, 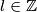
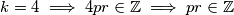
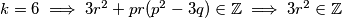
Dakle, sada znamo 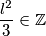 , pa
, pa 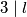 , pa je
, pa je 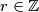 čime smo gotovi sa zadatkom.
čime smo gotovi sa zadatkom.
Ocjene: (1)
Komentari:
andrija004, 25. listopada 2020. 20:25
 Školjka
Školjka  je normirani polinom trećeg stupnja sa nultočkama
je normirani polinom trećeg stupnja sa nultočkama 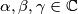 . Ako za svaki
. Ako za svaki  vrijedi to da
vrijedi to da 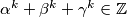 , dokaži da su onda svi koeficijenti od
, dokaži da su onda svi koeficijenti od