Točno
26. svibnja 2022. 17:10 (3 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 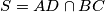 . Lagano se pokaže da su zbog ovih omjera
. Lagano se pokaže da su zbog ovih omjera 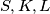 kolinearne. Neka je
kolinearne. Neka je  drugi presjek kružnice
drugi presjek kružnice 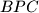 i
i 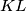 , te neka leži na dužini
, te neka leži na dužini 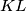 .
.
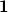 :
: 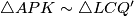
Vrijedi 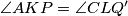 (presječnica 2 paralelna pravca). Nadalje,
(presječnica 2 paralelna pravca). Nadalje, 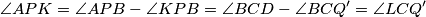 , te su po KK poučku ta 2 trokuta slična.
, te su po KK poučku ta 2 trokuta slična. 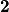 :
: 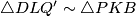
Opet vrijedi 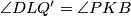 . Vrijedi sljedeći niz ekvivalencija:
. Vrijedi sljedeći niz ekvivalencija: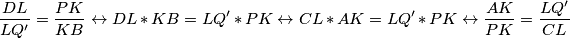 ,no zadnja jednakost je istinita zbog prethodno navedene sličnosti i tvrdnja je dokazana jer su navedeni trokuti slični po SKS poučku.
,no zadnja jednakost je istinita zbog prethodno navedene sličnosti i tvrdnja je dokazana jer su navedeni trokuti slični po SKS poučku.
Konačno, 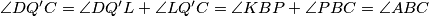 pa je
pa je 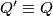 (postoji najviše 1 točka na dužini
(postoji najviše 1 točka na dužini 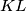 takva da
takva da 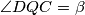 )
)
 Školjka
Školjka  be a trapezoid with parallel sides
be a trapezoid with parallel sides 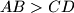 . Points
. Points  and
and  lie on the line segments
lie on the line segments  and
and  , respectively, so that
, respectively, so that 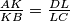 . Suppose that there are points
. Suppose that there are points  and
and  on the line segment
on the line segment 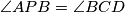 and
and 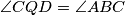 . Prove that the points
. Prove that the points  and
and  are concylic.
are concylic.