Točno
11. travnja 2022. 11:47 (3 godine, 10 mjeseci)
Let

be the orthocenter of an acute-angled triangle

. The circle
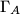
centered at the midpoint of

and passing through

intersects the sideline

at points
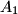
and
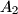
. Similarly, define the points
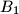
,
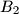
,
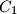
and
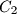
.
Prove that six points
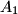
,
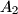
,
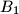
,
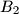
,
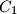
and
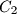
are concyclic.
Author: Andrey Gavrilyuk, Russia
%V0
Let $H$ be the orthocenter of an acute-angled triangle $ABC$. The circle $\Gamma_{A}$ centered at the midpoint of $BC$ and passing through $H$ intersects the sideline $BC$ at points $A_{1}$ and $A_{2}$. Similarly, define the points $B_{1}$, $B_{2}$, $C_{1}$ and $C_{2}$.
Prove that six points $A_{1}$ , $A_{2}$, $B_{1}$, $B_{2}$, $C_{1}$ and $C_{2}$ are concyclic.
Author: Andrey Gavrilyuk, Russia
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Postavimo $ABC$ na jediničnu kružnicu kompleksne ravnine. Neka je $M$ polovište $BC$, dokazat ćemo da je centar tražene kružnice centar opisane kružnice $ABC$. Uvjeti na $a_1$ su:
\[|a_1-m|=|h-m|\]
\[b+c=a_1+bc\overline{a_1}\]
Kvadriranjem prvog uvjeta i izmnažanjem dobiva se:
\[(a_1-\frac{b+c}{2})(\overline{a_1}-\frac{b+c}{2bc})=\frac{2a+b+c}{2}\cdot \frac{2bc+ab+ac}{2abc}\]
Ponovnim izmnažanjem imamo:
\[RHS=a_1\overline{a_1}-\frac{b+c}{2bc}(b+c-bc\overline{a_1})-\frac{b+c}{2}\overline{a_1}+\frac{(b+c)^2}{4bc}=a_1\overline{a_1}-\frac{(b+c)^2}{4bc}\]
Prebacivanjem konstante imamo konačno:
\[|a_1|^2=\frac{(2a+b+c)(2bc+ab+ac)+a(b+c)^2}{4abc}=\frac{8abc+4\sum_{sym}a^2b}{4abc}\], što je simetrično u $a,b,c$, što dokazuje našu tvrdnju, stoga sve tražene točke leže na kružnici s centrom $O$
 na jediničnu kružnicu kompleksne ravnine. Neka je
na jediničnu kružnicu kompleksne ravnine. Neka je  polovište
polovište  , dokazat ćemo da je centar tražene kružnice centar opisane kružnice
, dokazat ćemo da je centar tražene kružnice centar opisane kružnice  . Uvjeti na
. Uvjeti na  su:
su: 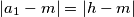
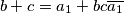 Kvadriranjem prvog uvjeta i izmnažanjem dobiva se:
Kvadriranjem prvog uvjeta i izmnažanjem dobiva se: 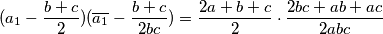 Ponovnim izmnažanjem imamo:
Ponovnim izmnažanjem imamo: 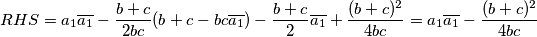 Prebacivanjem konstante imamo konačno:
Prebacivanjem konstante imamo konačno: 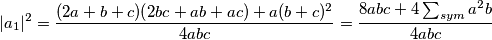 , što je simetrično u
, što je simetrično u  , što dokazuje našu tvrdnju, stoga sve tražene točke leže na kružnici s centrom
, što dokazuje našu tvrdnju, stoga sve tražene točke leže na kružnici s centrom 
 Školjka
Školjka  be the orthocenter of an acute-angled triangle
be the orthocenter of an acute-angled triangle 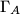 centered at the midpoint of
centered at the midpoint of 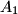 and
and 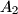 . Similarly, define the points
. Similarly, define the points 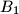 ,
, 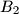 ,
, 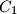 and
and 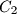 .
.