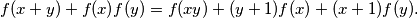Neka 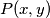 označava uvrštavanje
označava uvrštavanje  i
i  u početnu jednadžbu:
u početnu jednadžbu:
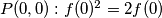
Ako 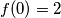 ,
, 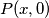 daje
daje 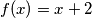 , što nije rješenje, zbog čega
, što nije rješenje, zbog čega 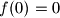
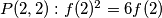 (
( )
)
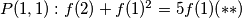
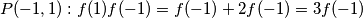
Ako 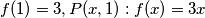 što je stvarno rješenje, zato nadalje neka je
što je stvarno rješenje, zato nadalje neka je 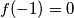
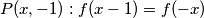
Sad, iz  i
i 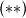 imamo 4 mogućnosti:
imamo 4 mogućnosti:
a)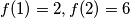
b)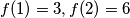
c)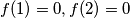
d)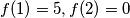
za b) slučaj 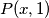 daje
daje 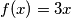 , ali to ne vrijedi za
, ali to ne vrijedi za  , pa nema rješenja ovdje
, pa nema rješenja ovdje
za d) slučaj 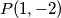 daje
daje 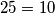 što očito ne vrijedi
što očito ne vrijedi
za c) slučaj 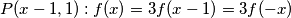 , iz čega lagano dobijamo
, iz čega lagano dobijamo 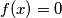 što je rješenje.
što je rješenje.
ostao je još samo a) slučaj
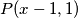 daje
daje 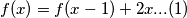
sada, usporedbom 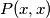 i
i 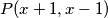 te korištenjem
te korištenjem  dobivamo
dobivamo 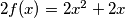 , odnosno
, odnosno 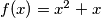 , što je isto rješenje.
, što je isto rješenje.
Sva rješenja su sada dana sa:
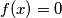
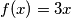
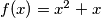
Provjerom se vidi da sve funkcije iznad zadovoljavaju.
Neka $P(x,y)$ označava uvrštavanje $x$ i $y$ u početnu jednadžbu:\\
$P(0,0): f(0)^2=2f(0)$\\
Ako $f(0)=2$, $P(x,0)$ daje $f(x)=x+2$, što nije rješenje, zbog čega $f(0)=0$\\
$P(2,2): f(2)^2=6f(2)$ ($*$)\\
$P(1,1): f(2)+f(1)^2=5f(1) (**)$\\
$P(-1,1): f(1)f(-1)=f(-1)+2f(-1)=3f(-1)$\\
Ako $f(1)=3, P(x,1): f(x)=3x$ što je stvarno rješenje, zato nadalje neka je $f(-1)=0$\\
$P(x,-1): f(x-1)=f(-x)$\\
Sad, iz $(*)$ i $(**)$ imamo 4 mogućnosti:\\
a)$f(1)=2,f(2)=6$\\
b)$f(1)=3,f(2)=6$\\
c)$f(1)=0,f(2)=0$\\
d)$f(1)=5,f(2)=0$\\
za b) slučaj $P(x,1)$ daje $f(x)=3x$, ali to ne vrijedi za $-1$, pa nema rješenja ovdje\\
za d) slučaj $P(1,-2)$ daje $25=10$ što očito ne vrijedi\\
za c) slučaj $P(x-1,1): f(x)=3f(x-1)=3f(-x)$, iz čega lagano dobijamo $f(x)=0$ što je rješenje.\\
ostao je još samo a) slučaj\\
$P(x-1,1)$ daje $f(x)=f(x-1)+2x...(1)$\\
sada, usporedbom $P(x,x)$ i $P(x+1,x-1)$ te korištenjem $(1)$ dobivamo $2f(x)=2x^2+2x$, odnosno $f(x)=x^2+x$, što je isto rješenje.\\
Sva rješenja su sada dana sa:\\
$f(x)=0$\\
$f(x)=3x$\\
$f(x)=x^2+x$\\
Provjerom se vidi da sve funkcije iznad zadovoljavaju.
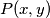 označava uvrštavanje
označava uvrštavanje  i
i  u početnu jednadžbu:
u početnu jednadžbu: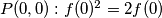
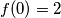 ,
, 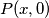 daje
daje 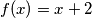 , što nije rješenje, zbog čega
, što nije rješenje, zbog čega 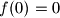
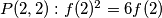 (
( )
)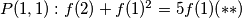
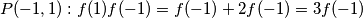
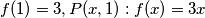 što je stvarno rješenje, zato nadalje neka je
što je stvarno rješenje, zato nadalje neka je 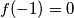
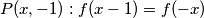
 i
i 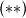 imamo 4 mogućnosti:
imamo 4 mogućnosti: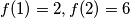
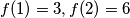
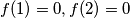
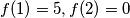
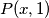 daje
daje 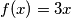 , ali to ne vrijedi za
, ali to ne vrijedi za  , pa nema rješenja ovdje
, pa nema rješenja ovdje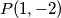 daje
daje 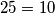 što očito ne vrijedi
što očito ne vrijedi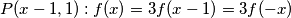 , iz čega lagano dobijamo
, iz čega lagano dobijamo 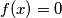 što je rješenje.
što je rješenje.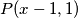 daje
daje 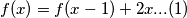
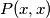 i
i 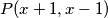 te korištenjem
te korištenjem  dobivamo
dobivamo 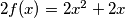 , odnosno
, odnosno 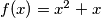 , što je isto rješenje.
, što je isto rješenje.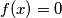
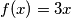
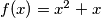
 Školjka
Školjka 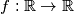 such that for all
such that for all 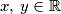 , we have
, we have