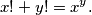Pomoćna lemma: 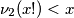 za sve prirodne
za sve prirodne 
Dokaz: Iz Legendreove formule:
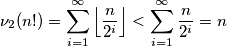
Također, 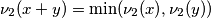 kad god
kad god 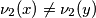
Ako je  neparan, zbog parnosti je ili
neparan, zbog parnosti je ili 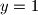 ili
ili  . Obje mogućnosti brzo vode na kontradikciju. Od sada nadalje
. Obje mogućnosti brzo vode na kontradikciju. Od sada nadalje  je paran. Razlikujemo 5 slučajeva:
je paran. Razlikujemo 5 slučajeva:
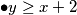
Lako je vidljivo da 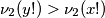
Također, 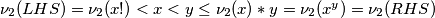 , kontradikcija
, kontradikcija
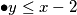
Slično prethodnom: 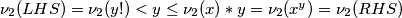 , kontradikcija
, kontradikcija
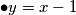
Dobiva se 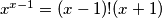 , no
, no  i
i  su relativno prosti i veći od 1, ponovno kontradikcija
su relativno prosti i veći od 1, ponovno kontradikcija
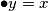
ovdje 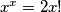 . Ako je
. Ako je 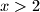 ,
,  ima prostog djelitelja, a on ne može dijeliti
ima prostog djelitelja, a on ne može dijeliti  , kontradikcija.
, kontradikcija. 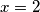 daje rješenje
daje rješenje 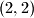
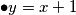
Ovdje je 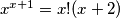 . Završava se kao i prethodni slučaj, te dobivamo rješenje
. Završava se kao i prethodni slučaj, te dobivamo rješenje 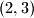
Iscrpili smo sve slučajeve, pa su jedina rješenja 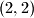 i
i 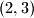
Pomoćna lemma: $\nu_2(x!)<x$ za sve prirodne $x$\\
Dokaz: Iz Legendreove formule:
\[ \nu_2(n!)=\sum_{i=1}^{\infty} \left \lfloor{\frac{n}{2^i}}\right \rfloor < \sum_{i=1}^{\infty} \frac{n}{2^i} = n\]
Također, $\nu_2(x+y)=\min(\nu_2(x),\nu_2(y))$ kad god $\nu_2(x) \neq \nu_2(y)$
Ako je $x$ neparan, zbog parnosti je ili $y=1$ ili $x=1$. Obje mogućnosti brzo vode na kontradikciju. Od sada nadalje $x$ je paran.
Razlikujemo 5 slučajeva:\\
$\bullet y \geq x+2$ \\
Lako je vidljivo da $\nu_2(y!)>\nu_2(x!)$ \\
Također, $\nu_2(LHS)=\nu_2(x!)<x<y \leq \nu_2(x)*y=\nu_2(x^y)=\nu_2(RHS)$, kontradikcija\\
$\bullet y \leq x-2$\\
Slično prethodnom:
$\nu_2(LHS)=\nu_2(y!)<y \leq \nu_2(x)*y=\nu_2(x^y)=\nu_2(RHS)$, kontradikcija\\
$\bullet y=x-1$\\
Dobiva se $x^{x-1}=(x-1)!(x+1)$, no $x+1$ i $x$ su relativno prosti i veći od 1, ponovno kontradikcija
$\bullet y=x$\\
ovdje $x^x=2x!$. Ako je $x>2$, $x-1$ ima prostog djelitelja, a on ne može dijeliti $x$, kontradikcija. $x=2$ daje rješenje $(2,2)$
$\bullet y=x+1$\\
Ovdje je $x^{x+1}=x!(x+2)$. Završava se kao i prethodni slučaj, te dobivamo rješenje $(2,3)$
Iscrpili smo sve slučajeve, pa su jedina rješenja $(2,2)$ i $(2,3)$
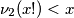 za sve prirodne
za sve prirodne 
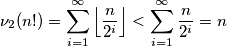
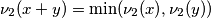 kad god
kad god 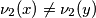
 neparan, zbog parnosti je ili
neparan, zbog parnosti je ili 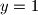 ili
ili  . Obje mogućnosti brzo vode na kontradikciju. Od sada nadalje
. Obje mogućnosti brzo vode na kontradikciju. Od sada nadalje  je paran. Razlikujemo 5 slučajeva:
je paran. Razlikujemo 5 slučajeva: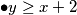
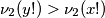
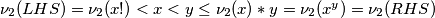 , kontradikcija
, kontradikcija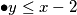
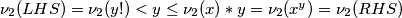 , kontradikcija
, kontradikcija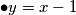
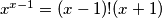 , no
, no  i
i  su relativno prosti i veći od 1, ponovno kontradikcija
su relativno prosti i veći od 1, ponovno kontradikcija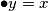
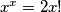 . Ako je
. Ako je 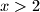 ,
,  ima prostog djelitelja, a on ne može dijeliti
ima prostog djelitelja, a on ne može dijeliti  , kontradikcija.
, kontradikcija. 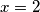 daje rješenje
daje rješenje 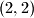
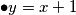
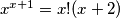 . Završava se kao i prethodni slučaj, te dobivamo rješenje
. Završava se kao i prethodni slučaj, te dobivamo rješenje 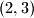
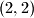 i
i 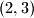
 Školjka
Školjka  of positive integers satisfying the equation
of positive integers satisfying the equation