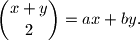Bez smanjenja općenitosti neka je 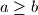 . Imamo 2 mogućnosti:
. Imamo 2 mogućnosti:
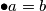
Ovdje samo uzmemo 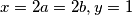 , te vrijedi
, te vrijedi 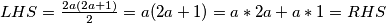
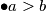
Neka je 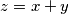 . Raspisivanjem uvjeta dobiva se:
. Raspisivanjem uvjeta dobiva se:
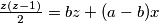
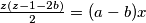
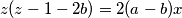
Ekvivalentno,
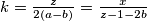 , za neki racionalni
, za neki racionalni 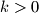
Sada, 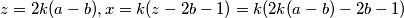
Kako 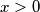 , mora biti
, mora biti 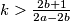
Isto tako, 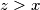 što daje redom:
što daje redom:
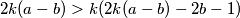
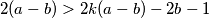
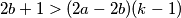
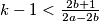
Nakon ovih ograda izbor  je gotovo očit, stavljamo
je gotovo očit, stavljamo 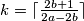
Kako je 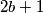 neparan, a
neparan, a 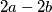 paran,
paran, 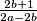 nije prirodan broj te vrijede gore navedene ograde. Također,
nije prirodan broj te vrijede gore navedene ograde. Također,  je prirodan pa su
je prirodan pa su  i
i  oba prirodni, odnosno
oba prirodni, odnosno  i
i  oba prirodni, te su svi uvjeti zadovoljeni
oba prirodni, te su svi uvjeti zadovoljeni
Bez smanjenja općenitosti neka je $a \geq b$. Imamo 2 mogućnosti:\\
$\bullet a=b$\\
Ovdje samo uzmemo $x=2a=2b, y=1$, te vrijedi $LHS=\frac{2a(2a+1)}{2}=a(2a+1)=a*2a+a*1=RHS$\\
$\bullet a>b$\\
Neka je $z=x+y$. Raspisivanjem uvjeta dobiva se:\\
$\frac{z(z-1)}{2}=bz+(a-b)x$\\
$\frac{z(z-1-2b)}{2}=(a-b)x$\\
$z(z-1-2b)=2(a-b)x$\\
Ekvivalentno,\\
$k=\frac{z}{2(a-b)}=\frac{x}{z-1-2b}$, za neki racionalni $k>0$\\
Sada, $z=2k(a-b), x=k(z-2b-1)=k(2k(a-b)-2b-1)$\\
Kako $x>0$, mora biti $k>\frac{2b+1}{2a-2b}$\\
Isto tako, $z>x$ što daje redom:\\
$2k(a-b)>k(2k(a-b)-2b-1)$\\
$2(a-b)>2k(a-b)-2b-1$\\
$2b+1>(2a-2b)(k-1)$\\
$k-1<\frac{2b+1}{2a-2b}$\\
Nakon ovih ograda izbor $k$ je gotovo očit, stavljamo $k=\lceil \frac{2b+1}{2a-2b} \rceil$\\
Kako je $2b+1$ neparan, a $2a-2b$ paran, $\frac{2b+1}{2a-2b}$ nije prirodan broj te vrijede gore navedene ograde.
Također, $k$ je prirodan pa su $x$ i $z$ oba prirodni, odnosno $x$ i $y$ oba prirodni, te su svi uvjeti zadovoljeni
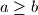 . Imamo 2 mogućnosti:
. Imamo 2 mogućnosti: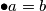
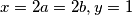 , te vrijedi
, te vrijedi 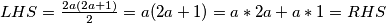
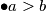
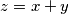 . Raspisivanjem uvjeta dobiva se:
. Raspisivanjem uvjeta dobiva se: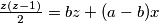
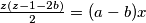
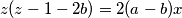
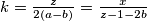 , za neki racionalni
, za neki racionalni 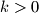
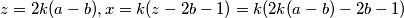
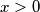 , mora biti
, mora biti 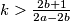
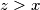 što daje redom:
što daje redom: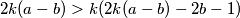
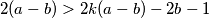
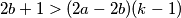
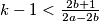
 je gotovo očit, stavljamo
je gotovo očit, stavljamo 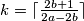
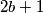 neparan, a
neparan, a 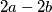 paran,
paran, 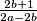 nije prirodan broj te vrijede gore navedene ograde. Također,
nije prirodan broj te vrijede gore navedene ograde. Također,  je prirodan pa su
je prirodan pa su  i
i  oba prirodni, odnosno
oba prirodni, odnosno  i
i  oba prirodni, te su svi uvjeti zadovoljeni
oba prirodni, te su svi uvjeti zadovoljeni  Školjka
Školjka  i
i  prirodni brojevi. Dokaži da postoje prirodni brojevi
prirodni brojevi. Dokaži da postoje prirodni brojevi