Točno
19. travnja 2012. 21:36 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Takav skup  postoji.
postoji.
Proizvoljno povežemo plave i zelene točke.
Ako nema sjecišta, gotovi smo.
Inače promatramo zbroj duljina svih dužina skupa
duljina svih dužina skupa  . Pokazat ćemo da čim se neke dvije dužine skupa
. Pokazat ćemo da čim se neke dvije dužine skupa  sijeku,
sijeku,  se može transformirati u skup s manjim zbrojem
se može transformirati u skup s manjim zbrojem  .
.
Odaberimo jedan par dužina i
i  skupa
skupa  , koje se sijeku u točki
, koje se sijeku u točki  , gdje su
, gdje su  i
i  zelene točke, a
zelene točke, a  i
i  plave točke. Sada možemo zamijeniti te dužine dužinama
plave točke. Sada možemo zamijeniti te dužine dužinama 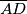 i
i  . Nakon toga će se ukupna duljina svih dužina skratiti, jer imamo:
. Nakon toga će se ukupna duljina svih dužina skratiti, jer imamo: 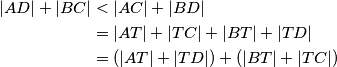 što slijedi iz nejednakosti trokuta
što slijedi iz nejednakosti trokuta 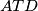 i
i 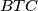 .
.
Kako može poprimiti samo konačno mnogo vrijednosti (postoji konačno mnogo sparivanja plavih i zelenih točaka), zaključujemo da se nakon konačno mnogo navedenih transformacija bilo koji početni skup
može poprimiti samo konačno mnogo vrijednosti (postoji konačno mnogo sparivanja plavih i zelenih točaka), zaključujemo da se nakon konačno mnogo navedenih transformacija bilo koji početni skup  može dovesti u skup
može dovesti u skup 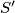 u kojem više nije moguće smanjiti
u kojem više nije moguće smanjiti  transformacijom. No, to znači da
transformacijom. No, to znači da 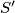 nema sjecišta.
nema sjecišta.
 postoji.
postoji.Proizvoljno povežemo plave i zelene točke.
Ako nema sjecišta, gotovi smo.
Inače promatramo zbroj
 duljina svih dužina skupa
duljina svih dužina skupa  . Pokazat ćemo da čim se neke dvije dužine skupa
. Pokazat ćemo da čim se neke dvije dužine skupa  sijeku,
sijeku,  se može transformirati u skup s manjim zbrojem
se može transformirati u skup s manjim zbrojem  .
.Odaberimo jedan par dužina
 i
i  skupa
skupa  , koje se sijeku u točki
, koje se sijeku u točki  , gdje su
, gdje su  i
i  zelene točke, a
zelene točke, a  i
i  plave točke. Sada možemo zamijeniti te dužine dužinama
plave točke. Sada možemo zamijeniti te dužine dužinama 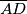 i
i  . Nakon toga će se ukupna duljina svih dužina skratiti, jer imamo:
. Nakon toga će se ukupna duljina svih dužina skratiti, jer imamo: 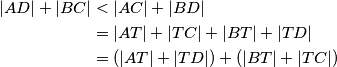 što slijedi iz nejednakosti trokuta
što slijedi iz nejednakosti trokuta 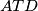 i
i 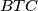 .
.Kako
 može poprimiti samo konačno mnogo vrijednosti (postoji konačno mnogo sparivanja plavih i zelenih točaka), zaključujemo da se nakon konačno mnogo navedenih transformacija bilo koji početni skup
može poprimiti samo konačno mnogo vrijednosti (postoji konačno mnogo sparivanja plavih i zelenih točaka), zaključujemo da se nakon konačno mnogo navedenih transformacija bilo koji početni skup  može dovesti u skup
može dovesti u skup 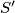 u kojem više nije moguće smanjiti
u kojem više nije moguće smanjiti  transformacijom. No, to znači da
transformacijom. No, to znači da 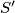 nema sjecišta.
nema sjecišta.  Školjka
Školjka  dano je
dano je  zelenih i
zelenih i