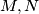
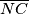
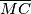
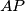
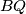
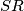
Upisana kružnica trokuta dodiruje stranice , i redom u točkama i . Neka je točka na manjem od dva luka i tangenta na taj luk s diralištem . Tangenta siječe i redom u točkama i . Dokažite da se pravci , , i sijeku u jednoj točki.
%V0
Upisana kružnica trokuta $ABC$ dodiruje stranice $\overline{AC}$, $\overline{BC}$ i $\overline{AB}$ redom u točkama $M, N$ i $R$. Neka je $S$ točka na manjem od dva luka $MN$ i $t$ tangenta na taj luk s diralištem $S$. Tangenta $t$ siječe $\overline{NC}$ i $\overline{MC}$ redom u točkama $P$ i $Q$. Dokažite da se pravci $AP$, $BQ$, $SR$ i $MN$ sijeku u jednoj točki.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Neka je . Dovoljno je kolinearno jer se analogno dokazuje . Međutim, ako označimo , Pascal na degenerirani sesterokut daje kolinearno, a na daje kolinearno. Spajanjem te 2 relacije tvrdnja je dokazana
Neka je $T=RS \cap MN$. Dovoljno je $A T P$ kolinearno jer se analogno dokazuje $B, T, Q$.
Međutim, ako označimo $L=SM \cap RN$, Pascal na degenerirani sesterokut $RSSMNN$ daje $T, P, L$ kolinearno, a na $RRSMMN$ daje $A, T, L$ kolinearno. Spajanjem te 2 relacije tvrdnja je dokazana
Školjka 
dodiruje stranice 
, 
i 
redom u točkama 
i 
. Neka je 
točka na manjem od dva luka 
i 
tangenta na taj luk s diralištem 
i 
redom u točkama 
i 
. Dokažite da se pravci 
, 
, 
i 
. Dovoljno je 
kolinearno jer se analogno dokazuje 
. Međutim, ako označimo 
, Pascal na degenerirani sesterokut 
daje 
kolinearno, a na 
daje 
kolinearno. Spajanjem te 2 relacije tvrdnja je dokazana