Točno
26. svibnja 2022. 22:22 (3 godine, 8 mjeseci)
Let

be a trapezoid with parallel sides
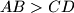
. Points

and

lie on the line segments

and

, respectively, so that
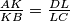
. Suppose that there are points

and

on the line segment
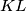
satisfying
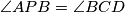
and
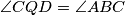
. Prove that the points

,

,

and

are concylic.
%V0
Let $ABC$ be a trapezoid with parallel sides $AB > CD$. Points $K$ and $L$ lie on the line segments $AB$ and $CD$, respectively, so that $\frac {AK}{KB} = \frac {DL}{LC}$. Suppose that there are points $P$ and $Q$ on the line segment $KL$ satisfying $\angle{APB} = \angle{BCD}$ and $\angle{CQD} = \angle{ABC}$. Prove that the points $P$, $Q$, $B$ and $C$ are concylic.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Po obratu Talesa, $AD$, $BC$, i $KL$ sijeku se u jednoj tocki $X$. Zelimo $XC*XB=XQ*XP$
$\angle BPA=\angle BCD$ i $\angle BPA + \angle DQC =180^{\circ}$ se mogu upotrijebiti istovremeno uvodenjem tocke $R$ kao tocka na duzini ${LX}$ takva da je $\angle {CRD}= \angle {BPA}$. Ovo je zgodno jer je onda ${DQCR}$ tetivan i $\angle{CRQ}=\angle{BCQ}$ pa je $XC^2=XR*XQ$. Zbog homoteticnosti je jasno da je ${DR}||{AP}$ i ${CR}||{BP}$, iz druge od te dvije paralelnosti zajedno s prijasnjom jednakosti slijedi $XC*XB=XQ*XP$.
| 28. svibnja 2022. 19:14 | 11235 | Točno |
 ,
,  , i
, i 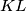 sijeku se u jednoj tocki
sijeku se u jednoj tocki  . Zelimo
. Zelimo 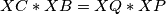
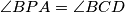 i
i 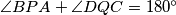 se mogu upotrijebiti istovremeno uvodenjem tocke
se mogu upotrijebiti istovremeno uvodenjem tocke  kao tocka na duzini
kao tocka na duzini 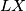 takva da je
takva da je 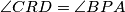 . Ovo je zgodno jer je onda
. Ovo je zgodno jer je onda 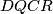 tetivan i
tetivan i 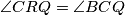 pa je
pa je 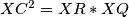 . Zbog homoteticnosti je jasno da je
. Zbog homoteticnosti je jasno da je 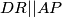 i
i 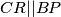 , iz druge od te dvije paralelnosti zajedno s prijasnjom jednakosti slijedi
, iz druge od te dvije paralelnosti zajedno s prijasnjom jednakosti slijedi 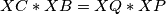 .
.  Školjka
Školjka  be a trapezoid with parallel sides
be a trapezoid with parallel sides 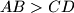 . Points
. Points  and
and  lie on the line segments
lie on the line segments  and
and  , respectively, so that
, respectively, so that 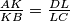 . Suppose that there are points
. Suppose that there are points  and
and  on the line segment
on the line segment 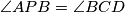 and
and 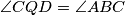 . Prove that the points
. Prove that the points  and
and  are concylic.
are concylic.