Točno
28. kolovoza 2022. 22:33 (3 godine, 6 mjeseci)
Korisnik: EMissoni
Zadatak: Školsko/gradsko natjecanje iz matematike 2015, SŠ1 A 6 (Sakrij tekst zadatka)
Zadatak: Školsko/gradsko natjecanje iz matematike 2015, SŠ1 A 6 (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
n^2 + 2n + 2015 = k^2 n^2 + 2n + 1 + 2014 = k^2 (n + 1)^2 + 2014 = k^2
neka je a = n + 1
a^2 + 2014 = k^2 2014 = k^2 - a^2 2014 = (k - a)(k + a)
Sada ako je (k - a)(k + a) dijeljiv sa 2 (Sto je jer je 2014 = 2 * 1007) Sad barem jedan od (k - a) i (k + a) mora biti dijeljiv sa 2
1) (k - a) je dijeljiv sa 2 2|(k - a) 2|2a
2|(k - a) + 2a 2|k + a ako 2 dijeli k - a onda 2 dijeli i k + a
2) (k + a) je dijeljiv sa 2 2|(k + a) 2|2a
2|(k + a) - 2a 2|k - a ako 2 dijeli k + a onda 2 dijeli i k - a
Znači da ako 2 dijeli (k - a)(k + a) onda nužno i 4 dijeli (k - a)(k + a), kako 4 ne dijeli 2014 ne postoji takav n.
Ocjene: (1)
Komentari:
MatejVojvodic1505, 1. rujna 2022. 17:29
 Školjka
Školjka  takav da je
takav da je 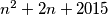 kvadrat nekog prirodnog broja?
kvadrat nekog prirodnog broja? 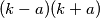 mora biti djeljiv s
mora biti djeljiv s  na brži način samo mi se nije dalo editat lol
na brži način samo mi se nije dalo editat lol 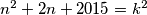
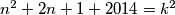
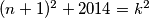
 si mogao puno brže i lakše obrazložiti tako da si samo promatrao da
si mogao puno brže i lakše obrazložiti tako da si samo promatrao da  i
i  moraju biti iste parnosti.
moraju biti iste parnosti.