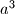
Dekadski zapis prirodnog broja ima znamenaka, a dekadski zapis broja ima znamenaka. Je li moguće da je ?
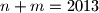
%V0
Dekadski zapis prirodnog broja $a$ ima $n$ znamenaka, a dekadski zapis broja $a^3$ ima $m$ znamenaka. Je li moguće da je $n+m=2013$?
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Ukoliko ima znamenaka, onda može imati najmanje znamenaka (npr. ako je ), odnosno najviše znamenaka (npr. ako je ).
Provjerimo svaki od slučajeva:
1. ; slijedi
2. ; slijedi
3. ; slijedi
Ni u kojem od slučajeva, nije prirodan. Dakle, nije moguće.
Ukoliko $a$ ima $n$ znamenaka, onda $a^3$ može imati najmanje $3(n-1)+1$ znamenaka (npr. ako je $a=1000\dots$), odnosno najviše $3n$ znamenaka (npr. ako je $a=9999\dots$).
Provjerimo svaki od slučajeva:
1. $m = 3n-2$; slijedi $4n-2 = 2013$
2. $m = 3n-1$; slijedi $4n-1 = 2013$
3. $m = 3n$; slijedi $4n = 2013$
Ni u kojem od slučajeva, $n$ nije prirodan. Dakle, nije moguće.
Školjka 
ima 
znamenaka, a dekadski zapis broja 
ima 
znamenaka. Je li moguće da je 
? 
znamenaka (npr. ako je 
), odnosno najviše 
znamenaka (npr. ako je 
).
; slijedi 
; slijedi 
; slijedi 