Metoda posljednje znamenke je samo poseban slučaj metode kongruencija kojom ćemo se pozabaviti neki drugi put koristeći kao uvod predavanje s ovogodišnje Ljetne škole: https://drive.google.com/drive/folders/170lvUaNcIh_BsNTtRsrZHARXhKRW2-4t?usp=sharing
PRIMJER 1:
Riješi diofantsku jednadžbu 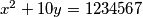 .
.
RJEŠENJE:
Kvadrat cijelog broja može završavati jednom od znamenaka 0, 1, 4, 5, 6 ili 9. S obzirom da 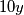 završava znamenkom 0, zadnja znamenka od
završava znamenkom 0, zadnja znamenka od 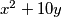 može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
PRIMJER 2:
Riješimo diofantsku jednadžbu 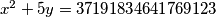 .
.
RJEŠENJE:
Budući da kvadrat cijelog broja završava sa znamenkom 0, 1, 4, 5, 6, ili 9,a broj 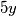 sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
Zadatci za samostalno rješavanje
1. Nađi sve parove prirodnih brojeva 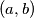 takvih da vrijedi:
takvih da vrijedi: 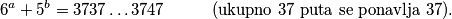
2. Nađite cjelobrojna rješenja jednadžbe: 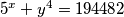 .
.
Kliknite ovdje kako biste prikazali rješenje.
1. Zadatak Uočimo da će zadnja znamenka broja 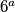 za
za 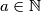 biti
biti  i također uočimo isto i za
i također uočimo isto i za 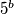 da je zadnja znamenka
da je zadnja znamenka  što bi značilo da če njihov zbroj imati zadnju znamenku
što bi značilo da če njihov zbroj imati zadnju znamenku  što dokazuje da jednađba
što dokazuje da jednađba 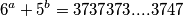 Nema prirodnih rješenja.
Nema prirodnih rješenja.
2. Zadatak Opet primjetimo zadnja znamenka broja 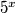 je
je  , a zadnje znamenke broja
, a zadnje znamenke broja 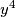 mogu biti
mogu biti  ,
,  ili
ili  kako god da ih zbrojimo nečemo dobiti da je zadnja znamenka broj
kako god da ih zbrojimo nečemo dobiti da je zadnja znamenka broj  . Što znači da nema cjelobrojnih rješenja.
. Što znači da nema cjelobrojnih rješenja.
 Školjka
Školjka ![y_{1/2} = \pm \sqrt[4]{194481}](/media/m/f/d/2/fd21a7ea9c0f9928cce26f074c9f756a.png)
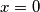 imati rješenja! I to dva! Samo ih treba naći :)
imati rješenja! I to dva! Samo ih treba naći :)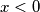 nema rješenja (npr. ... zbog zatvorenost cijelih brojeva na zbrajanje/oduzimanje/množenje).
nema rješenja (npr. ... zbog zatvorenost cijelih brojeva na zbrajanje/oduzimanje/množenje).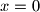 bi moglo biti jedno rješenje, a za
bi moglo biti jedno rješenje, a za 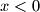 nema rješenja
nema rješenja cjelobrojan, ne smijemo direktno zaključiti da broj
cjelobrojan, ne smijemo direktno zaključiti da broj