MatesV13, 22. listopada 2022. 19:28
Patrlk, 22. listopada 2022. 19:24
Pa mislim možemo dokazat i da je $$V(a , b) = gcd(a , b)a_1b_1$$ i bez ove jednakosti mislim da dokaz koji sam čitao u nekoj knjizi o teoriji brojeva ide ovako.
$$V(a , b) = ak_1$$
$$V(a , b) = bk_2$$
$$V(a , b) = gcd(a , b)a_1k_1$$
$$V(a , b) = gcd(a , b)b_1k_2$$
Prema tome
$$a_1k_1 = b_1k_2$$
Zato što $a_1$ ne djeli $b_1$ onda $a_1$ djeli $k_2$ ili ti
$$k_2 = a_1 \cdot k_3$$
Radi toga što tražimo najmanji zajednički višekratnik dobijamo da je $k_3 = 1$
$$k_2 = a_1$$
Odakle
$$V(a , b) = gcd(a , b)a_1b_1$$
Zadnja promjena:
Patrlk, 22. listopada 2022. 19:25
MatesV13, 22. listopada 2022. 19:11
Fali dosta stvari. Najprije, nigdje nisi naglasio da je 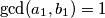 (iako je to standardna oznaka, treba negdje pisati).
(iako je to standardna oznaka, treba negdje pisati).
Nadalje, nije dobro reći da je 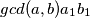 definicija najmanjeg zajedničkog višekratnika. To je zapravo posljedica točno jednakosti koju treba pokazati.
definicija najmanjeg zajedničkog višekratnika. To je zapravo posljedica točno jednakosti koju treba pokazati.
Za prirodne brojeve, definicija najvećeg zajedničkog djelitelja je "najveći prirodni broj koji dijeli oba broja", a najmanjeg zajedničkog višekratnika je "najmanji prirodni broj koji je djeljiv s oba broja". Sve osim toga su izvedenice iz te definicije, pa u dokazu treba paziti što se dokazuje iz čega (znači ne možemo reći da trivijalno vrijedi jer znamo da vrijedi).
Fali dosta stvari. Najprije, nigdje nisi naglasio da je $\gcd(a_1, b_1)=1$ (iako je to standardna oznaka, treba negdje pisati).
Nadalje, nije dobro reći da je $gcd(a , b)a_1b_1$ definicija najmanjeg zajedničkog višekratnika. To je zapravo posljedica točno jednakosti koju treba pokazati.
Za prirodne brojeve, definicija najvećeg zajedničkog djelitelja je "najveći prirodni broj koji dijeli oba broja", a najmanjeg zajedničkog višekratnika je "najmanji prirodni broj koji je djeljiv s oba broja". Sve osim toga su izvedenice iz te definicije, pa u dokazu treba paziti što se dokazuje iz čega (znači ne možemo reći da trivijalno vrijedi jer znamo da vrijedi).
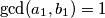 (iako je to standardna oznaka, treba negdje pisati).
(iako je to standardna oznaka, treba negdje pisati).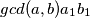 definicija najmanjeg zajedničkog višekratnika. To je zapravo posljedica točno jednakosti koju treba pokazati.
definicija najmanjeg zajedničkog višekratnika. To je zapravo posljedica točno jednakosti koju treba pokazati. Školjka
Školjka  i
i  vrijedi
vrijedi 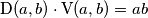 .
. 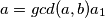
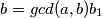
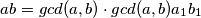
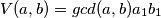 i bez ove jednakosti mislim da dokaz koji sam čitao u nekoj knjizi o teoriji brojeva ide ovako.
i bez ove jednakosti mislim da dokaz koji sam čitao u nekoj knjizi o teoriji brojeva ide ovako.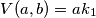
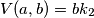
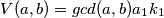
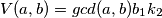 Prema tome
Prema tome 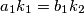 Zato što
Zato što  ne djeli
ne djeli 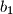 onda
onda  ili ti
ili ti 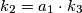 Radi toga što tražimo najmanji zajednički višekratnik dobijamo da je
Radi toga što tražimo najmanji zajednički višekratnik dobijamo da je 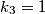
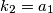 Odakle
Odakle