Točno
22. listopada 2022. 19:50 (1 godina, 6 mjeseci)
Odredi zbroj: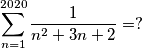 
Odredi zbroj: $$\sum_{n=1}^{2020}\frac{1}{n^2 + 3n + 2} = ?$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
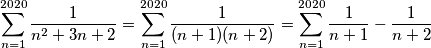
Ovo je bia primjer rako da znamo da je ta suma jednaka samo što je primjer počinjao sa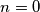 
ili nes tako
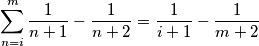
Ili ti vamo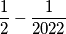 
$$\sum_{n=1}^{2020}\frac{1}{n^2 + 3n + 2} =\sum_{n=1}^{2020} \frac{1}{(n + 1)(n + 2)} = \sum_{n=1}^{2020} \frac{1}{n + 1} - \frac{1}{n + 2}$$
Ovo je bia primjer rako da znamo da je ta suma jednaka samo što je primjer počinjao sa $n = 0$ ili nes tako
$$\sum_{n=i}^{m} \frac{1}{n +1} - \frac{1}{n + 2} = \frac{1}{i + 1} - \frac{1}{m + 2}$$
Ili ti vamo
$$\frac{1}{2} - \frac{1}{2022}$$
Školjka