Točno
22. listopada 2022. 23:46 (1 godina, 6 mjeseci)
Odredi zbroj: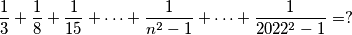 
Odredi zbroj: $$\frac{1}{3} + \frac{1}{8} + \frac{1}{15} + \dots + \frac{1}{n^2-1} + \dots + \frac{1}{2022^2 - 1} =?$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
$$\sum_{n=2}^{2022} \frac{1}{n^2 - 1} $$
$$\sum_{n=2}^{2022} \frac{1}{(n + 1)(n - 1)}$$
$$\sum_{n=2}^{2022} \frac{1}{2n - 2} - \frac{1}{2n + 2}$$
Promatrajmo taj niz
$$\left[ \frac{1}{2} - \frac{1}{6} \right] + \left[ \frac{1}{4} - \frac{1}{8} \right] + \left[ \frac{1}{6} - \frac{1}{10} \right] + \left[ \frac{1}{8} - \frac{1}{12} \right] + \left[ \frac{1}{10} - \frac{1}{14} \right] + ... + \left[ \frac{1}{4038} - \frac{1}{4042} \right] + \left[ \frac{1}{4040} - \frac{1}{4044} \right] + \left[ \frac{1}{4042} - \frac{1}{4046} \right]$$
Sad promotrimo da se sve skrati osim :
$$\frac{1}{2} + \frac{1}{4} - \frac{1}{4044} - \frac{1}{4046}$$
Školjka 
![\left[ \frac{1}{2} - \frac{1}{6} \right] + \left[ \frac{1}{4} - \frac{1}{8} \right] + \left[ \frac{1}{6} - \frac{1}{10} \right] + \left[ \frac{1}{8} - \frac{1}{12} \right] + \left[ \frac{1}{10} - \frac{1}{14} \right] + ... + \left[ \frac{1}{4038} - \frac{1}{4042} \right] + \left[ \frac{1}{4040} - \frac{1}{4044} \right] + \left[ \frac{1}{4042} - \frac{1}{4046} \right]](/media/m/d/9/b/d9b5046df98234e8ef653f52b50f5617.png)
