Točno
23. listopada 2022. 00:12 (1 godina, 6 mjeseci)
Neka je 
. Izračunaj sljedeću sumu: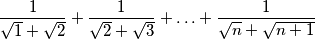 
Neka je $n \in \mathbb{N}$. Izračunaj sljedeću sumu:
$$\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\ldots +\frac{1}{\sqrt{n}+\sqrt{n+1}}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Idemo ovo racionalizirat ( u nazivniku ce uvijek biti 1)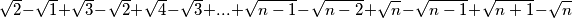 
Uočavamo da ce nam ostat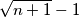 
Idemo ovo racionalizirat ( u nazivniku ce uvijek biti 1)
$$\sqrt{2} - \sqrt{1} + \sqrt{3} - \sqrt{2} + \sqrt{4} - \sqrt{3} + ... + \sqrt{n - 1} - \sqrt{n - 2} + \sqrt{n} - \sqrt{n - 1} + \sqrt{n + 1} - \sqrt{n}$$
Uočavamo da ce nam ostat
$$\sqrt{n + 1} - 1$$
Školjka