Točno
31. listopada 2022. 20:57 (3 godine, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
MatesV13, 31. listopada 2022. 21:31
 Školjka
Školjka 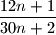 neskrativ za sve
neskrativ za sve  .
. 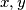 njihov najveći zajednički djelitelj je također djelitelj broja
njihov najveći zajednički djelitelj je također djelitelj broja 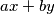 gdje su
gdje su 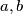 neki cjeli brojevi.
neki cjeli brojevi.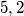
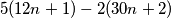
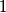 Ovo nam kaže da je najveći zajednički djelitelj također djelitelj broja
Ovo nam kaže da je najveći zajednički djelitelj također djelitelj broja  tako da je on isto
tako da je on isto