Neocijenjeno
18. veljače 2023. 23:06 (3 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Da bi rjesenja bila cijeli brojevi. 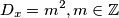 Onda imamo
Onda imamo
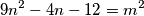
Opet stavimo
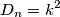
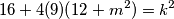
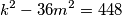
Bez gubitka opčenitosti neka su nam kvadrati pozitivni.
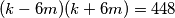
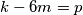
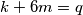
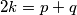
Jedini djelitelji broja 448 da je zbroj njihov djeljiv sa 2 su (14 , 32) , ( 28 , 16) , (56 , 8) , (112 , 4) , (228 , 2)
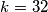 Je jedini za koji će n biti prirodan broj. Sad uvrstimo to da dobijemo
Je jedini za koji će n biti prirodan broj. Sad uvrstimo to da dobijemo 
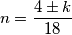 Uzimamo + jer je n prirodan broj. Tako da inamo
Uzimamo + jer je n prirodan broj. Tako da inamo 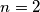
Što možemo provjeriti da vrijedi.
 Školjka
Školjka 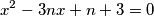 ima cjelobrojna rješenja.
ima cjelobrojna rješenja.