Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
Ok evo me nazad sa malo više znanja i pročitao sam zadatak.
2. 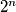 označava broj podskupova skupa sa n stvari. (Hoćemo li ili nećemo uzeti broj u skup , n puta)
označava broj podskupova skupa sa n stvari. (Hoćemo li ili nećemo uzeti broj u skup , n puta)
Sve podskupove možemo također dobiti ako od n elemenata uzmemo k elemenata od k = 0 do k = n.
3. U razredu sa n + 1 učenika stavimo jednog učenika kao predsjednika. I sad želimo poslat k učenika u ravnatelja. To možemo napravit tako da uzmemo k učenika od svih učenika bez predsjednika ili uzmemo k - 1 učenika sa predsjednikom.
Pa... ok, uistinu vrijedi, samo je to algebarski dokaz, ne kombinatornim argumentom XD
Dokaz kombinatornim argumentom bi išao nekako ovako: recimo da želim izabrati grupu od  natjecatelja iz razreda s
natjecatelja iz razreda s  učenika. Mogu direktno izabrati
učenika. Mogu direktno izabrati  natjecatelja na
natjecatelja na 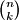 načina, ili mogu izabrati grupu od
načina, ili mogu izabrati grupu od 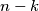 koji neće ići na natjecanje na
koji neće ići na natjecanje na  načina. Sada bi na natjecanju još trebalo pokazati bijekciju između tih načina (tj. svaki način koji bira grupu natjecatelja postoji jedinstven način koji bira nenatjecatelje i obratno) da bude skroz formalno.
načina. Sada bi na natjecanju još trebalo pokazati bijekciju između tih načina (tj. svaki način koji bira grupu natjecatelja postoji jedinstven način koji bira nenatjecatelje i obratno) da bude skroz formalno.
Više o dokazivanju kombinatornim argumentom ima ovdje: https://mnm.hr/wp-content/uploads/2015/10/Dokazivanje_kombinatornim_argumentom.pdf
 Školjka
Školjka 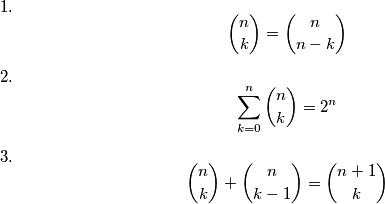
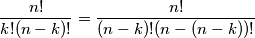 Očita istina
Očita istina