Kliknite ovdje kako biste prikazali rješenje.
Neka su  ,
,  i
i  presjeci
presjeci 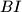 i
i 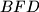 ,
, 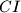 i
i 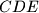 , te
, te 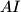 i
i 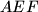 . Naravno,
. Naravno, 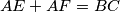 pa ćemo moći koristiti simetrične argumente za sve 3 kružnice.
pa ćemo moći koristiti simetrične argumente za sve 3 kružnice.
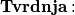
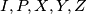 su na jednoj kružnici
su na jednoj kružnici
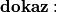 Najprije,
Najprije,  je na
je na 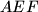 (Miquelov teorem, lagani chase). Dovoljno je pokazati da je
(Miquelov teorem, lagani chase). Dovoljno je pokazati da je 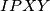 tetivan, analogno je
tetivan, analogno je 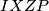 i
i 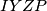 . Usmjereni kutevi daju:
. Usmjereni kutevi daju: 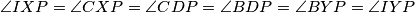 pa je
pa je 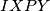 zaista tetivan. Sada ide glavna ideja zadatka, iskorištavanje čudnog uvjeta i razlog uvođenja presjeka sa simetralama:
zaista tetivan. Sada ide glavna ideja zadatka, iskorištavanje čudnog uvjeta i razlog uvođenja presjeka sa simetralama:
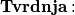 Položaji
Položaji 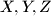 ne ovise o
ne ovise o 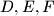 .
.
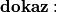 Dovoljno je pokazati da se
Dovoljno je pokazati da se 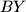 može izraziti preko veličina u trokutu
može izraziti preko veličina u trokutu  . Koristimo Ptolomejev teorem u četverokutu
. Koristimo Ptolomejev teorem u četverokutu 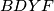 :
: 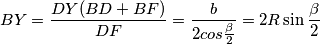 gdje smo koristili sinusov poučak u
gdje smo koristili sinusov poučak u 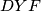 . Motivirano ovime, možemo naslutiti:
. Motivirano ovime, možemo naslutiti:
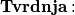
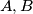 i
i  imaju istu potenciju na
imaju istu potenciju na 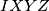
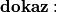 Dokazat ćemo da je
Dokazat ćemo da je 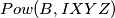 simetrično u
simetrično u  . Opet sinus na
. Opet sinus na 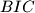 daje:
daje: 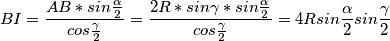 pa je
pa je 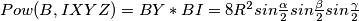 , što je uistinu simetrično u
, što je uistinu simetrično u  . Koristeći definiciju potencije točke, slijedi da su
. Koristeći definiciju potencije točke, slijedi da su 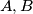 i
i  jednako udaljene od centra
jednako udaljene od centra 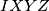 . Međutim, jedina točka koja je jednako udaljena od
. Međutim, jedina točka koja je jednako udaljena od 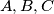 je
je  , iz čega slijedi da je
, iz čega slijedi da je  centar
centar 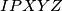 što završava.
što završava.
 Školjka
Školjka  . The points
. The points 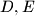 and
and  on the sides
on the sides 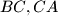 and
and  respectively are such that
respectively are such that 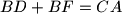 and
and 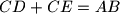 . The circumcircles of the triangles
. The circumcircles of the triangles 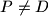 . Prove that
. Prove that 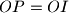 .
.